A ball weighing 15 g is tied to a string 10 cm long. Initially the ball is held in position such that the string is horizontal. The ball is now released. A nail N is situated vertically below the support at a distance L. The minimum value of L such that the string will be wound round the nail is :

2 cm
6 cm
4 cm
8 cm
The correct Answer is:B
Here the ball is released at A.
For the ball to just take a circular path about N (nail), the string at B must have zero tension.
mv2R=mg
or v=√gR
Also, mg=OB×12mv2orOB=v22g=gR2g=R2
∴10=R2+2R=5R2orR=4cm
Now L=OB+R=R2+R
=3R2=32×4cm+6cm

Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - LEVEL-III (MCQ)10videos
ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ8videos
ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ8videos
ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - RECENT COMPETITIVE QUESTION32videos
RAY OPTICS
- BOOK - MODERN PUBLICATIONCHAPTER - SOLIDS & SEMICONDUCTOR DEVICESEXERCISE - Revision Test28videos
SOLIDS & SEMICONDUCTOR DEVICES
Similar Questions
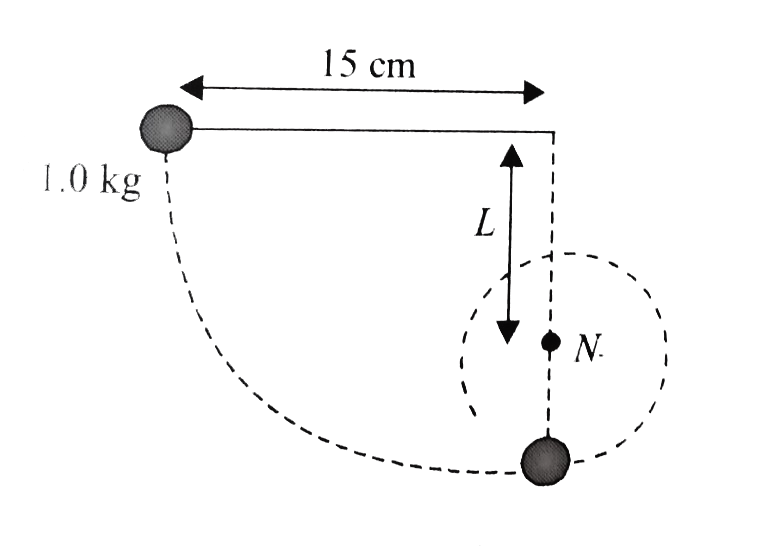
A ball weighing 1.0 kg is tied to a string 15 cm long initially the ball is held in position such that the string is horizontal. The ball is now released. A nail N is situated vertically below the support at a distance L. The minimum value of L such that the string will be would round the nail is.View SolutionA ball of mass 100 g is suspended by a string 40cm long. Keeping the string taut, the ball describes a horizontal circle of radius 10 cm. Find the angular speed.
View Solution
Knowledge Check
- Question 1 - Select One

A ball weighing 1.0 kg is tied to a string 15 cm long initially the ball is held in position such that the string is horizontal. The ball is now released. A nail N is situated vertically below the support at a distance L. The minimum value of L such that the string will be would round the nail is.A15 cmB4 cmC9 cmDNone of these
A ball is attached to a string of length L. The ball is released when the string is horizontal. The ball collides with wall and e=2/√5. After how many minimum number of collisions , the amplitude of oscillation becomes less than 60∘.
 View Solution
View Solution
A ball is attached to a string of length L and the ball is given velocity v0 at its lowest point. Find the speed of the ball at point B,C and D. Assume that the ball is moving in vertical circle.View SolutionA ball of mass 0.1kg is suspended by a string 30cm long Keeping the string always taut the ball describe a horizontal circle of radius 15cm Calculate the angular speed of the ball .
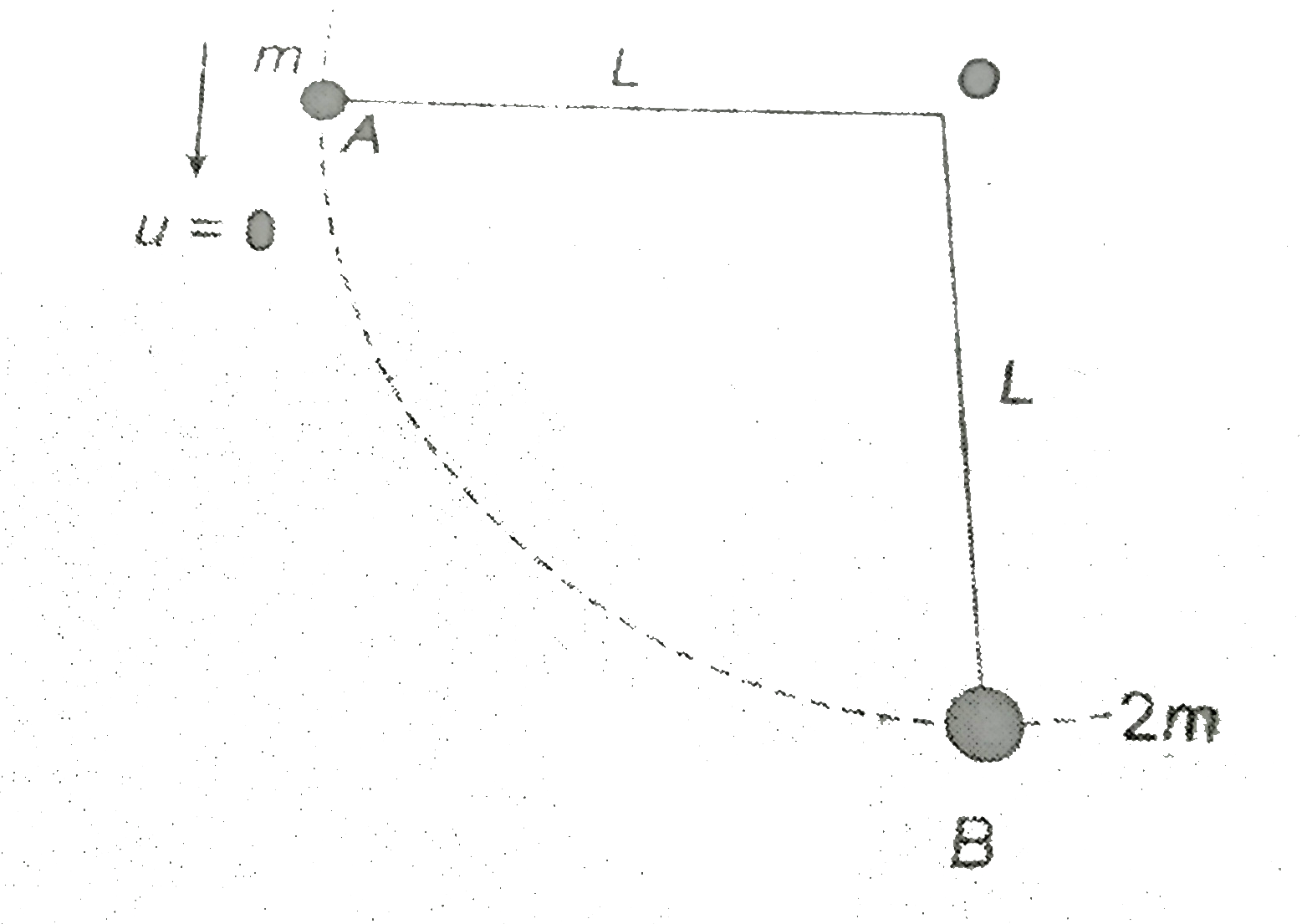
View SolutionA ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
 View Solution
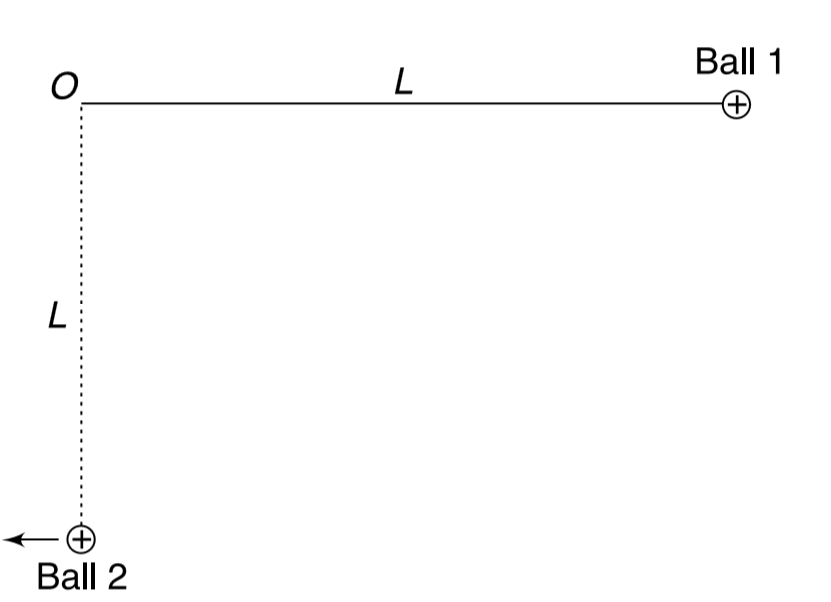
View SolutionA small positively charged ball of mass m is suspended by an insulating thread of length L. This ball remains in equilibrium with string horizontal when another small charged ball is placed exactly at a distance L below the point of suspension of the first ball. The second ball is slowly moved away from the first ball to a far away point. (The second ball is moved horizontally so that the first ball does not accelerate). As a result the first ball lowers down to the original position of the second ball and the string become vertical. Find the work done by the external agent in removing the second ball.
 View Solution
View SolutionA particle of mass 21 g attached to a string of 70cm length Keeping the string always taut the ball describes a horizontal circle of radius 15cm Calculate the angular speed of the ball .
View SolutionA simple pendulum consists of a ball of mass m connected to a string of length L. The ball is pulled aside so that the string makes an angle of 53∘ with the verticle and is released. Find the ratio of the minumum and the tension in the string.
View Solution

