A particle is placed at the origin and a force F = kx is acting on it (where k is a positive constant). If U (0) = 0, the graph of U (x) versus x will be (where U is the potential energy function) :




The correct Answer is:A
Since F =−dUdx=kx
∴dU=−Kxdx
or U=−Kxdx=−12Kx2
This is quadratic equation i.e., equation of a parabola. Thus correct choice is (a).
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - PROPERTIES OF MATTEREXERCISE - MULTIPLE CHOICE QUESTIONS (LEVEL-III)
13 Videos
- PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - PROPERTIES OF MATTEREXERCISE - RECENT COMPETITIVE QUESTIONS
17 Videos
- PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - PROPERTIES OF MATTEREXERCISE - RECENT COMPETITIVE QUESTIONS
17 Videos
- OSCILLATIONSBOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - RCQ
7 Videos
- RAY OPTICSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - RECENT COMPETITIVE QUESTION
32 Videos
Similar Questions
A particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
View SolutionA particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
View Solution
Knowledge Check
A particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
A B
B C
C D
D
A particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
A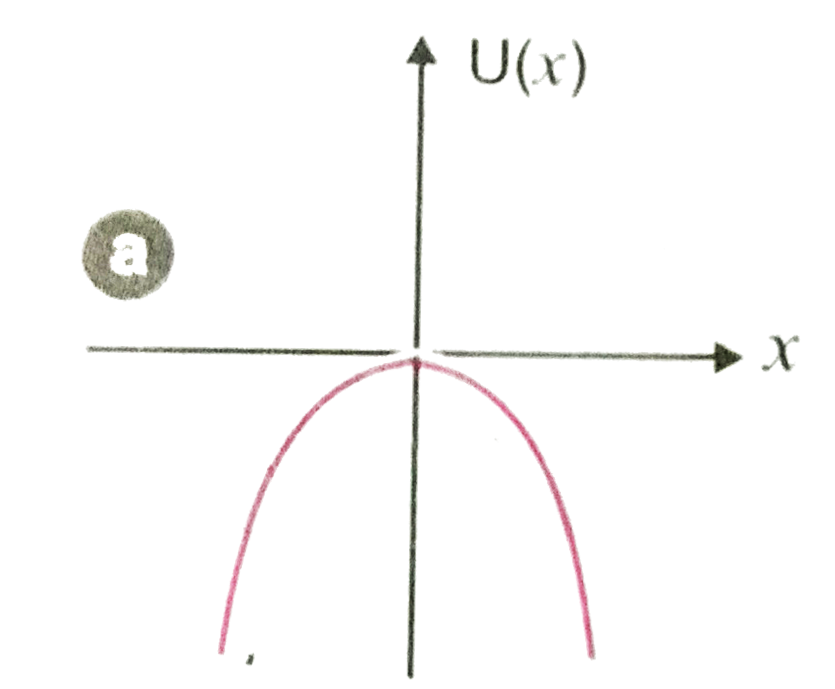 B
B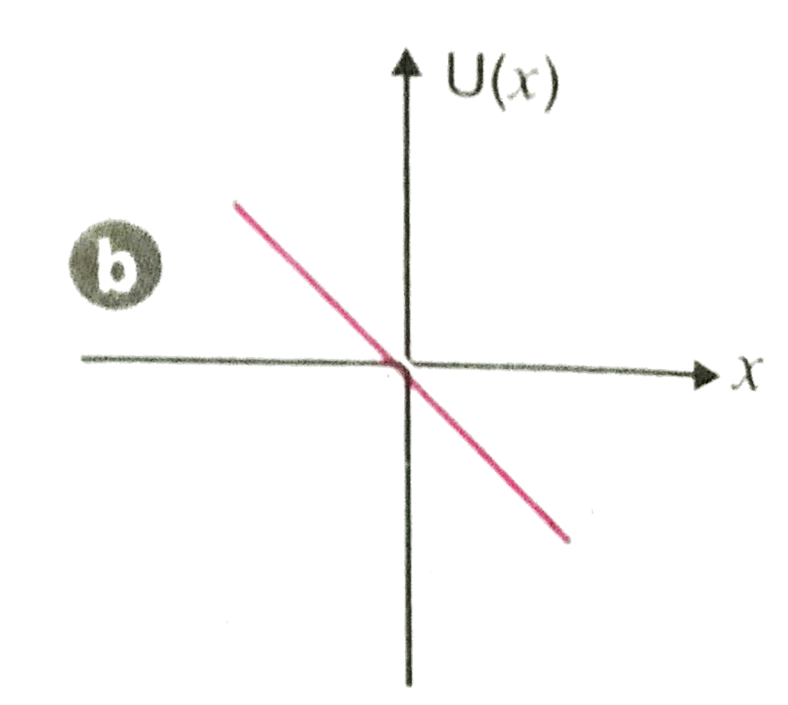 C
C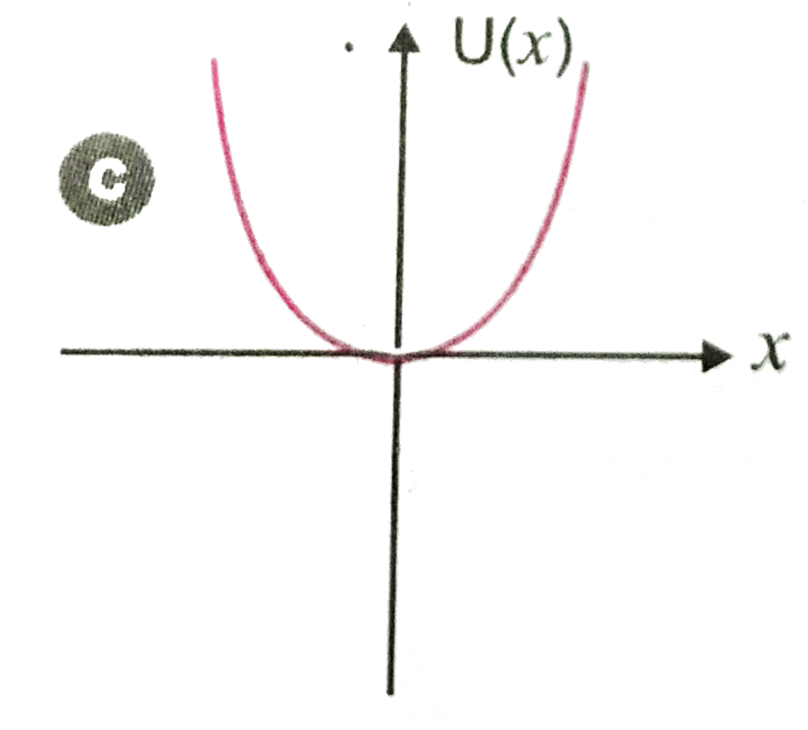 D
D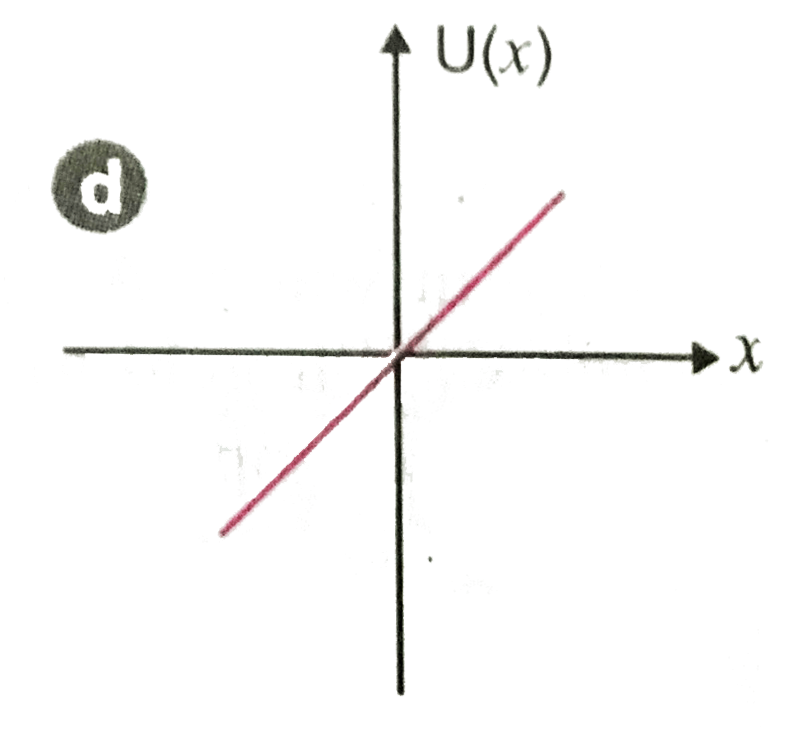
On a particle placed at origin a variable force F=−ax(where a is a positive constant) is applied. If U(0)=0, the graph between potential energy of particle U(x) and x is best represented by:-
A B
B C
C D
D
On a particle placed at origin a variable force F=−ax(where a is a positive constant) is applied. If U(0)=0, the graph between potential energy of particle U(x) and x is best represented by:-
View SolutionA particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with the distance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the particle is.
(a)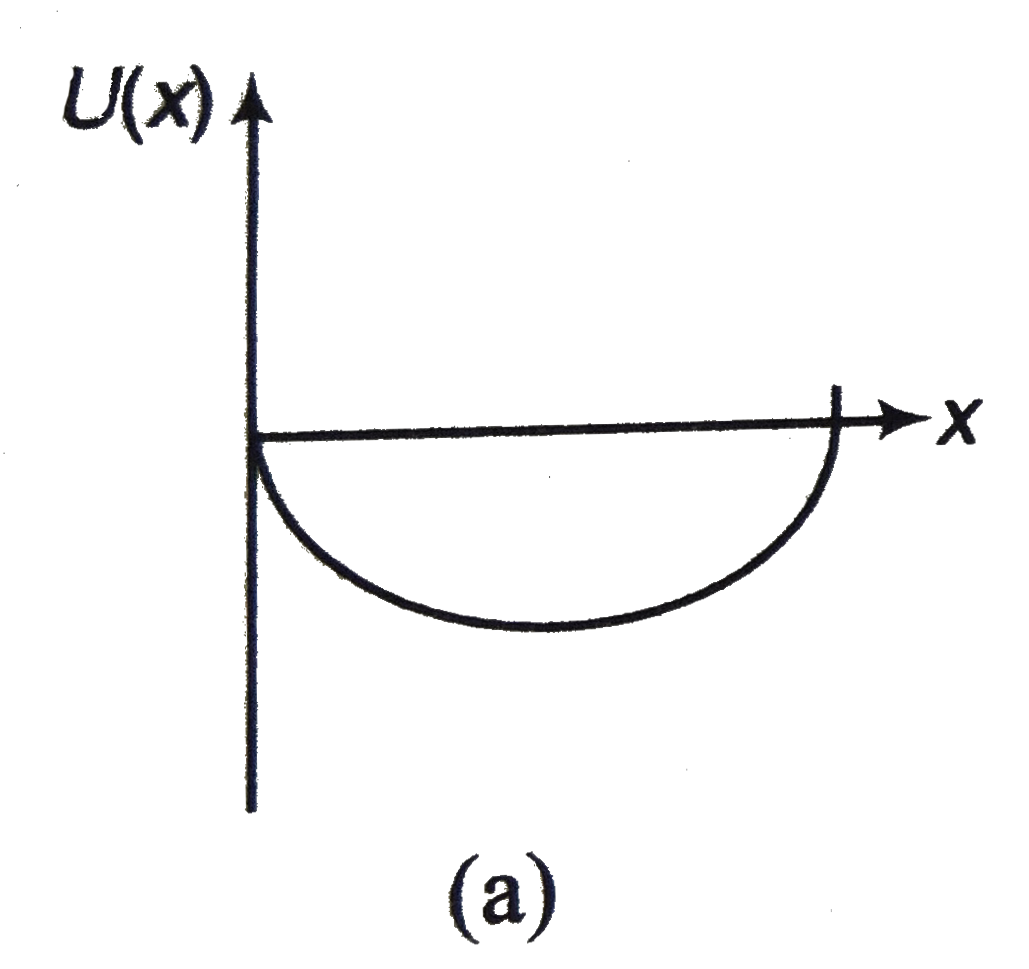 , (b)
, (b) 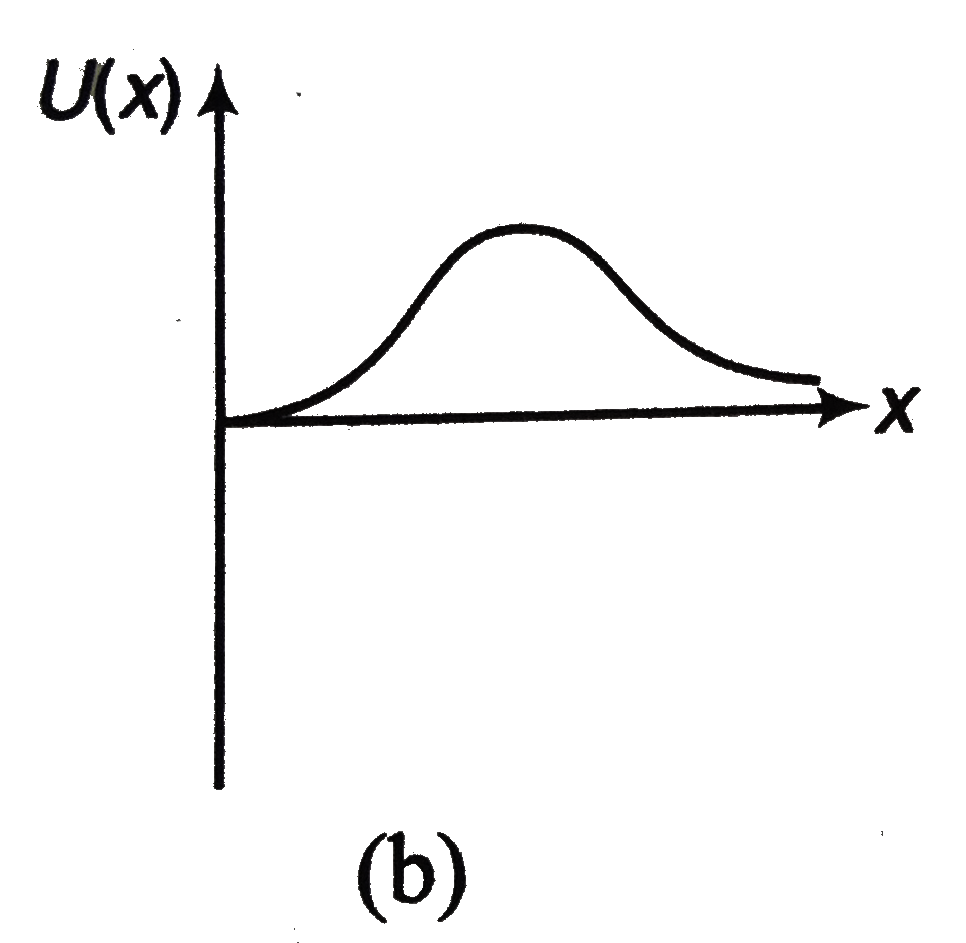 , (c)
, (c) 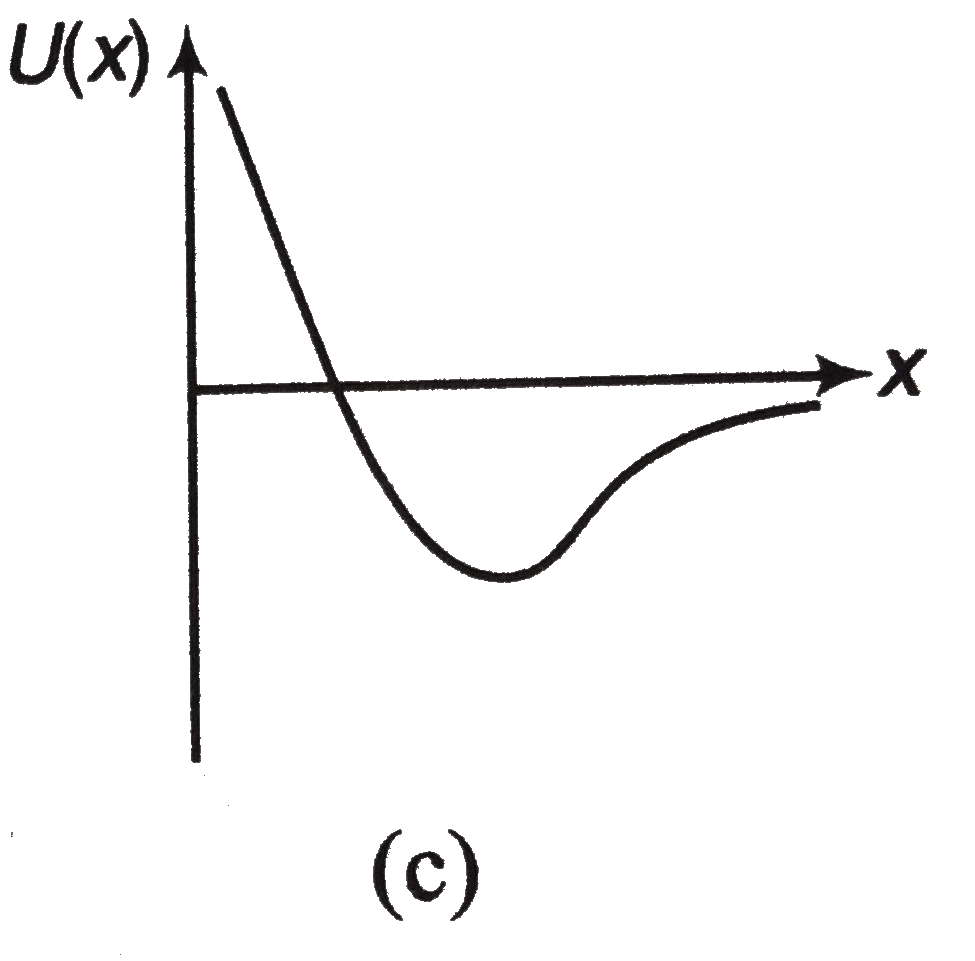 , (d)
, (d) 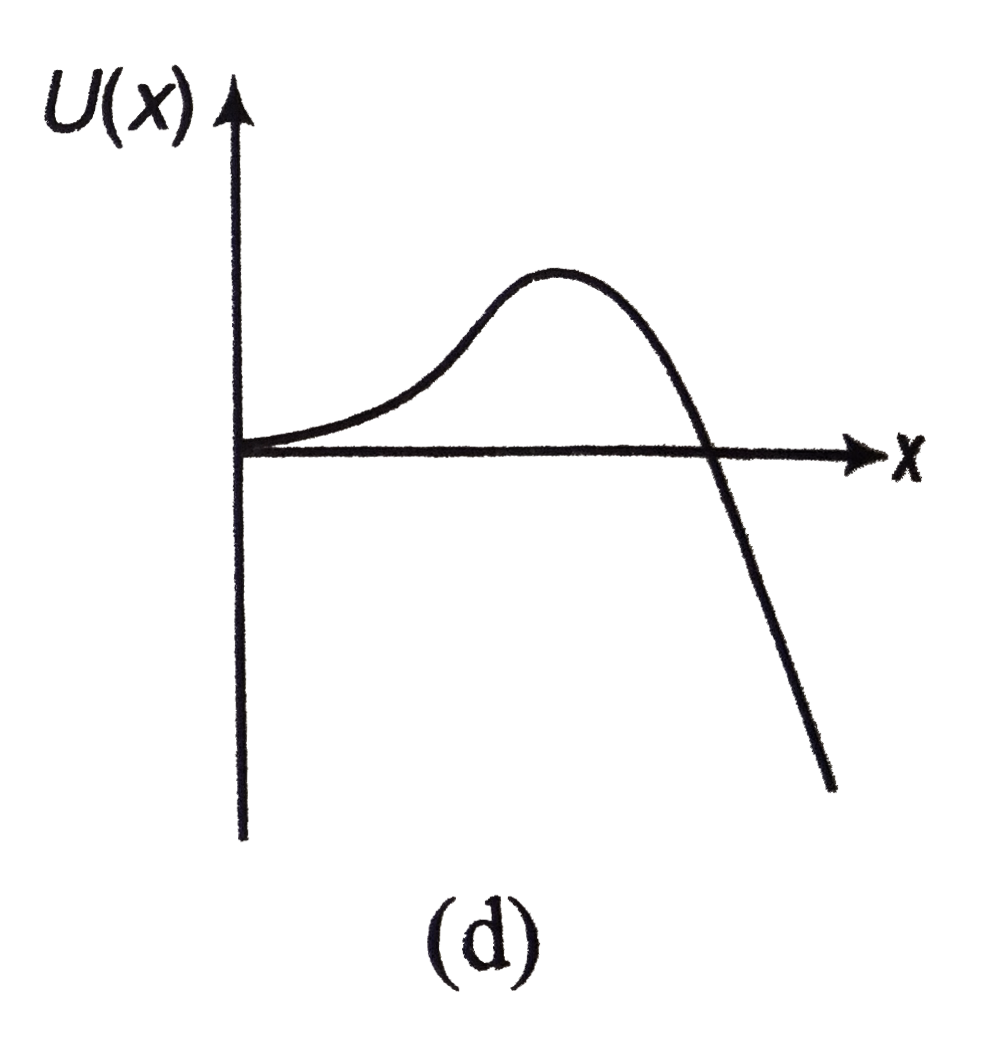 .
.
View SolutionA particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the porticle is.
(a) , (b)
, (b)  , (c)
, (c)  , (d)
, (d)  .
.
View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants.For ximplies0, the correct variation of potential energy function U(x) is best represented by.
View SolutionA particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x)=−kx+ax3. Here k and a are origin as F(x)=−kx+ax3. Here k and a are positive constants. For x=0, the functional form of the potential energy U(x) of particle is.
View Solution
