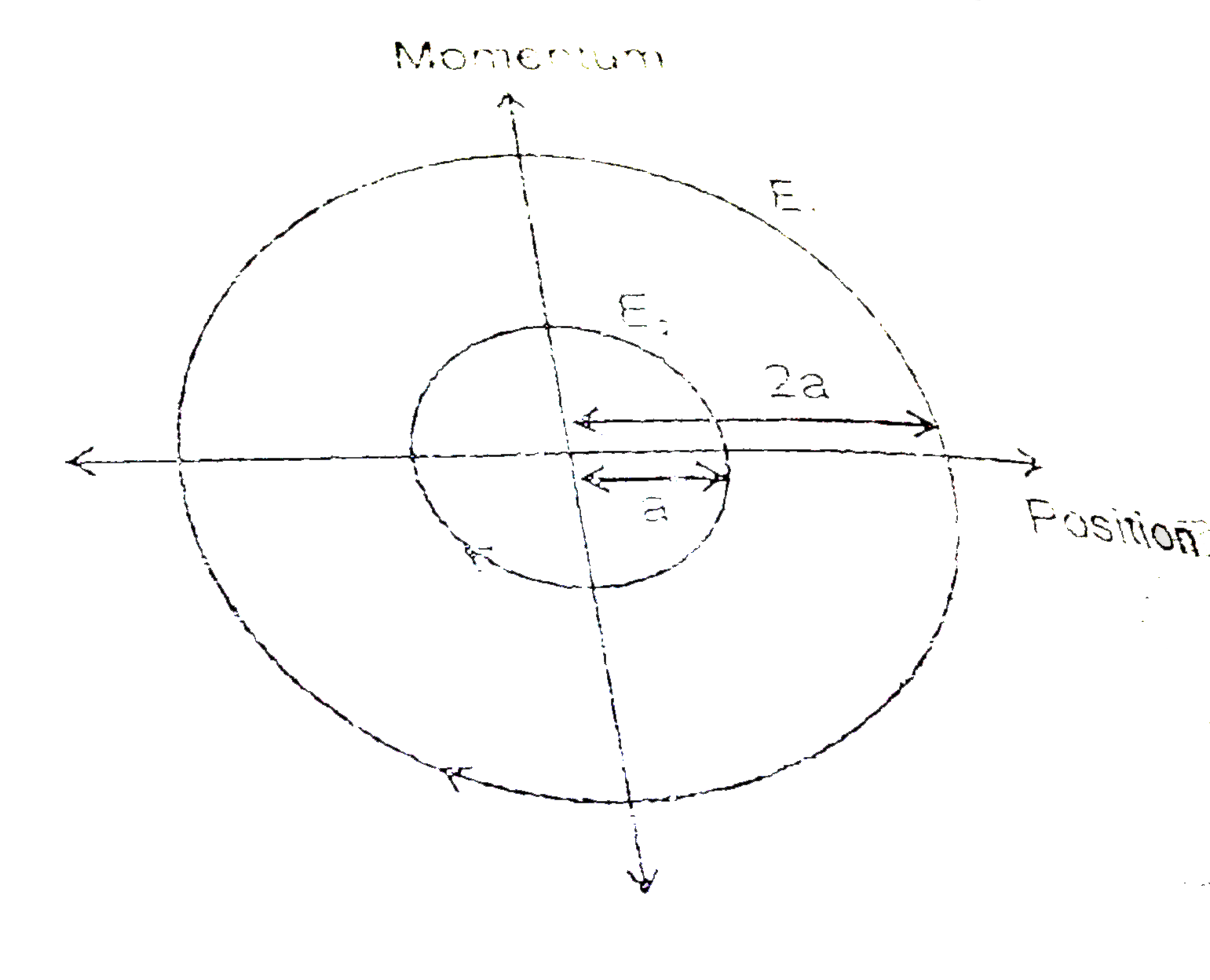
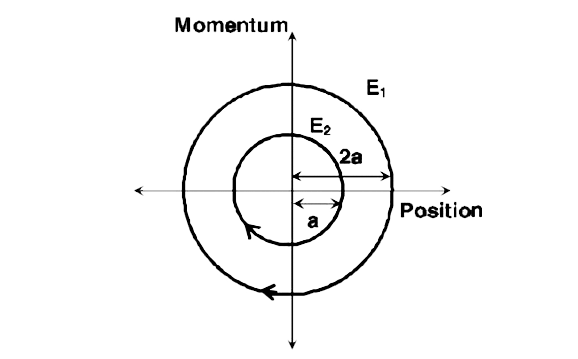
The phase space diagram for simple harmonic motion is a circle centered at the origin. In the figure, the two circles represent the same oscillator but for different initial conditions, and E1 and E2 are the total mechanical energies respectively. Then

E1=√2E2
E1=2E2
E1=4E2
E1=16E2
The correct Answer is:C
Since E∝A2
So, E1E2=(2a)2a2=4⇒E1=4E2.
So, correct choice is ( c ).
Topper's Solved these Questions
- OSCILLATIONSBOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - RCQ
7 Videos
- OSCILLATIONSBOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - MCQ (LEVEL-II)
62 Videos
- MOCK TEST-3BOOK - MODERN PUBLICATIONCHAPTER - MOCK TEST-3EXERCISE - MCQs
49 Videos
- PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - PROPERTIES OF MATTEREXERCISE - RECENT COMPETITIVE QUESTIONS
17 Videos
Similar Questions
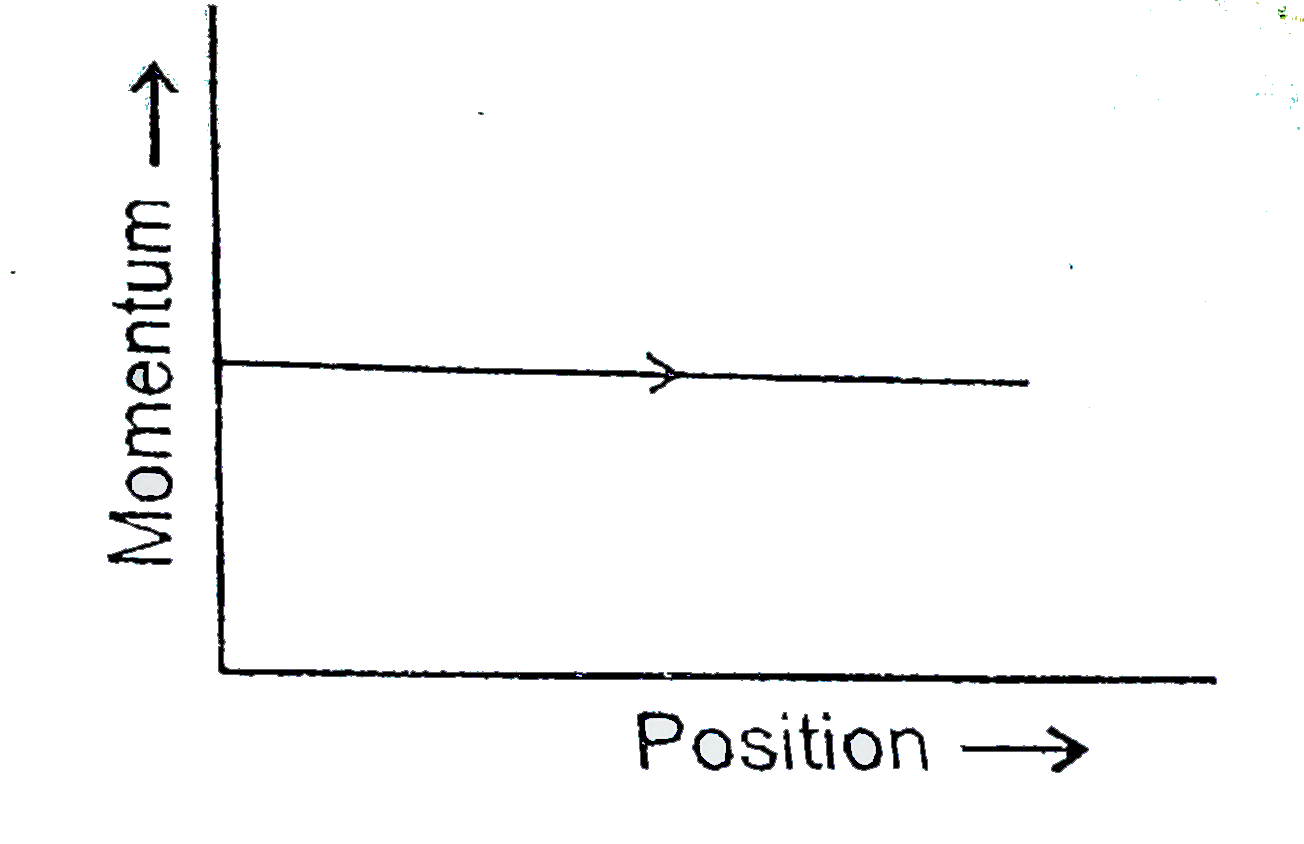
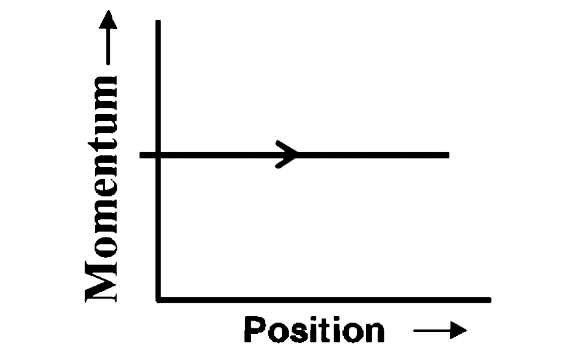
Phase space diagrams are useful tools in analysing all kond of dynamical problems. Theya re especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical system in one-dimelnsion. for such systeam, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. for example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which position or momentum. upwards (or to right) is positive and downwards (or to left) is negative.
The phase space diagram for simple harmonic motion is a circle cen-tered at the origin.In the figure, the two circles represent the same oscillator but for different initial conditions, and E1 for E2 are the total mechanical energies respectively. Then
View SolutionPhase space deagrams are useful tools
 .
.
in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
The plase space deagram for simple harmonic motion is a circle centered at the origin. In the figure, the two circles represent the same oscillator but for different initial condetions, and E_(1) and E_(2) the total mechanical energies respectivey.
 .
.
View Solution
Knowledge Check
Phase space diagrams are useful tools in analysing all kond of dynamical problems. Theya re especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical system in one-dimelnsion. for such systeam, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. for example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which position or momentum. upwards (or to right) is positive and downwards (or to left) is negative.

The phase space diagram for simple harmonic motion is a circle cen-tered at the origin.In the figure, the two circles represent the same oscillator but for different initial conditions, and E1 for E2 are the total mechanical energies respectively. Then
 AE1=√2E2BE1=2E2CE1=4E2DE1=16E2
AE1=√2E2BE1=2E2CE1=4E2DE1=16E2Phase space diagrams are useful tools in analysing all kond of dynamical problems. Theya re especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical system in one-dimelnsion. for such systeam, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. for example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which position or momentum. upwards (or to right) is positive and downwards (or to left) is negative.

The phase space diagram for simple harmonic motion is a circle cen-tered at the origin.In the figure, the two circles represent the same oscillator but for different initial conditions, and E1 for E2 are the total mechanical energies respectively. Then
 AE1=√2E2BE1=2E2CE1=4E2DE1=16E2
AE1=√2E2BE1=2E2CE1=4E2DE1=16E2A simple harmonic motion is represented by the equation, y = 5 sin π(t+4). Then the values of amplitude A and initial phase ∝ are respectively.
AA=5,∝=4πBA=10,∝=0CA=5,∝=0DA=10,∝=4π
The phase space diagram for harmonic motion is a circle centered at the origin as shown in figure. The to circles represent the same oscillator but for different initial conditions and E1 and E2 are the total mechanical energy, respectively . Then

View SolutionFigure represents two simple harmonic motions the parameter which has different value in the two motion is

View SolutionFigure represents two simple harmonic motions the parameter which has different value in the two motion is

View SolutionFind the phase difference between two particles executing simple harmonic motion with the same frequency if they are found inn the states shown in the figures at four different points of time.
View SolutionThe total energy of simple harmonic oscillator is E and amplitude is 'A'. It the kinetic energy is 3E/4 without altering the amplitude. The displacement of the oscillator is
View Solution
