Raed the following passage and and answer the following questions.
Stefan's law states that the ernergy emitted per second per unit area of the perfect black body is directly proportional to fourth power of its absolute temperature i.e. E∝T4 or E=σT4 where σ is called Stefan's constant. If the body is placed in enclosure maintained at temperature T0 then E=σ(T4−T40). If temperature difference between the body and the surroundings is very small then energy emitted per second per unit area of the body and surrounding i.e E∝(T−T0). This is known as Newton's Law of cooling and is a special case of Stefan's Law.
Two bodies P and Q are having equal surface areas and are maintained at temperature 17∘C and 27∘C respectively. Then radiant energy emitted per second are in the ratio of : Solution in Kannada
16:81
8:27
2:3
7:8
The correct Answer is:D
E1E2+σT41σT42=(290300)4=87=78
So correct choice is (d).
Topper's Solved these Questions
- TRANSFERENCE OF HEAT BOOK - MODERN PUBLICATIONCHAPTER - TRANSFERENCE OF HEAT EXERCISE - Multiple Choice Questions (Level - III) Questions From AIEEE/JEE Examination)
5 Videos
- TRANSFERENCE OF HEAT BOOK - MODERN PUBLICATIONCHAPTER - TRANSFERENCE OF HEAT EXERCISE - Recent Competitive Questions
4 Videos
- TRANSFERENCE OF HEAT BOOK - MODERN PUBLICATIONCHAPTER - TRANSFERENCE OF HEAT EXERCISE - Recent Competitive Questions
4 Videos
- SOLIDS & SEMICONDUCTOR DEVICESBOOK - MODERN PUBLICATIONCHAPTER - SOLIDS & SEMICONDUCTOR DEVICESEXERCISE - Revision Test
28 Videos
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Revision Test
57 Videos
Similar Questions
A composite block is made of slabs A,B,C,D and E of different thermal conductivities (given in terms of a constant K) and sizes (given in terms of length, L) as shown in the figure. All slabs are of same width. Heat 'Q' flows only from left to right through the blocks.
Then in steady state
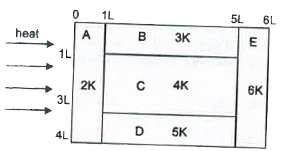
View SolutionTwo slabs are of the thicknesses d1 and d2. Their thermal conductivities are K1 and K2 respectively They are in series. The free ends of the combination of these two slabs are kept at temperatures θ1 and θ2. Assume θ1>θ2. The temperature θ of their common junction is
View SolutionTwo slabs are of the thicknesses d1 and d2. Their thermal conductivities are K1 and K2 respectively They are in series. The free ends of the combination of these two slabs are kept at temperatures θ1 and θ2. Assume θ1>θ2. The temperature θ of their common junction is
View SolutionChoose the forward biased p-n junction :
View SolutionA sphere of mass m is tied to end of a string of length 1 and rotated through the other and along a horizontal circular path with speed . The work done in full horizontal circle is:
View SolutionAccording to stefan's law of radiation a black body radiates energy σT4 from is unit surface area every second where T is the surface temperature of the black body and σ=5.67×10−8W/m2K4 is known as Stefan's of as a ball of radius 0.5m When detonated it reaches temperature of 106K and can be treated as a black body Estimate the power it radiates .
View SolutionPower emitted per unit area of a black body is R " watt/m"^(2) . At what wavelength will the power radiated by black body be maximum is stefan's constant is sigma and Wien's constant is b then.
View SolutionThe power emitted per unit area of a black body is R watt/m2. At what wavelength will the power radiated by the black body be maximum. If the Stefan's constant is σ and Wien's constant is b, then
View SolutionThe thermal radiation emitted by a body per second per unit area is (DeltaH)/(A Deltat)=kT^(4) . If sigma is Stefan's constant, then body
View Solutionकृष्णिका के विकरण-उत्सर्जन के लिए,स्टीफन का नियम Q∝T4है। E के मात्रक लिखिए।
View Solutionएक आदर्श कृष्णिका का ताप 1727∘C तथा क्षेत्रफल 0.1 मीटर2 है | कृष्णिका द्वारा प्रति मिनट उत्सर्जित विकिरण ऊर्जा की गणना कीजिये | स्टीफन नियतांक, σ=5.67×10−8 वाट/मीटर2−K4 |
View Solutionतप्त पिण्ड के लिये स्टीफन के नियम E=σT4 में E व्यक्त करता है -
View SolutionA body with surface area (A), temperature (T) and emissivity (e) = 0.6 is kept inside a spherical black body. What will be the maximum energy radiated ? [ sigma is Stefan's constant]
View SolutionA spherical body of emissivity e, placed inside a perfectly black body (emissivity = 1) is maintained at absolute temperature T. The energy radiated by a unit area of the body per second will be (σ is Stefan's constant)
View SolutionThe law which relates the energy radiated per second by unit area of a body and fourth power of absolute temperature of body is
View Solution
