Question

ABCD is a square of side ${\displaystyle l}$. A line parallel to the diagonal BD at a distance 'x' from the vertex A cuts two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x. Find this area at ${\displaystyle x=1/\sqrt{2}}$ and at ${\displaystyle x=2}$, when ${\displaystyle l=2}$.

Explanation

There are two cases
Case -I : when `x=AP le OA, i.e., x le (l)/(sqrt(2))`

` :. Ar(triangle AEF)=(1)/(2)x,2x=x^(2) " " ( :' PE =PF=AP=x)`
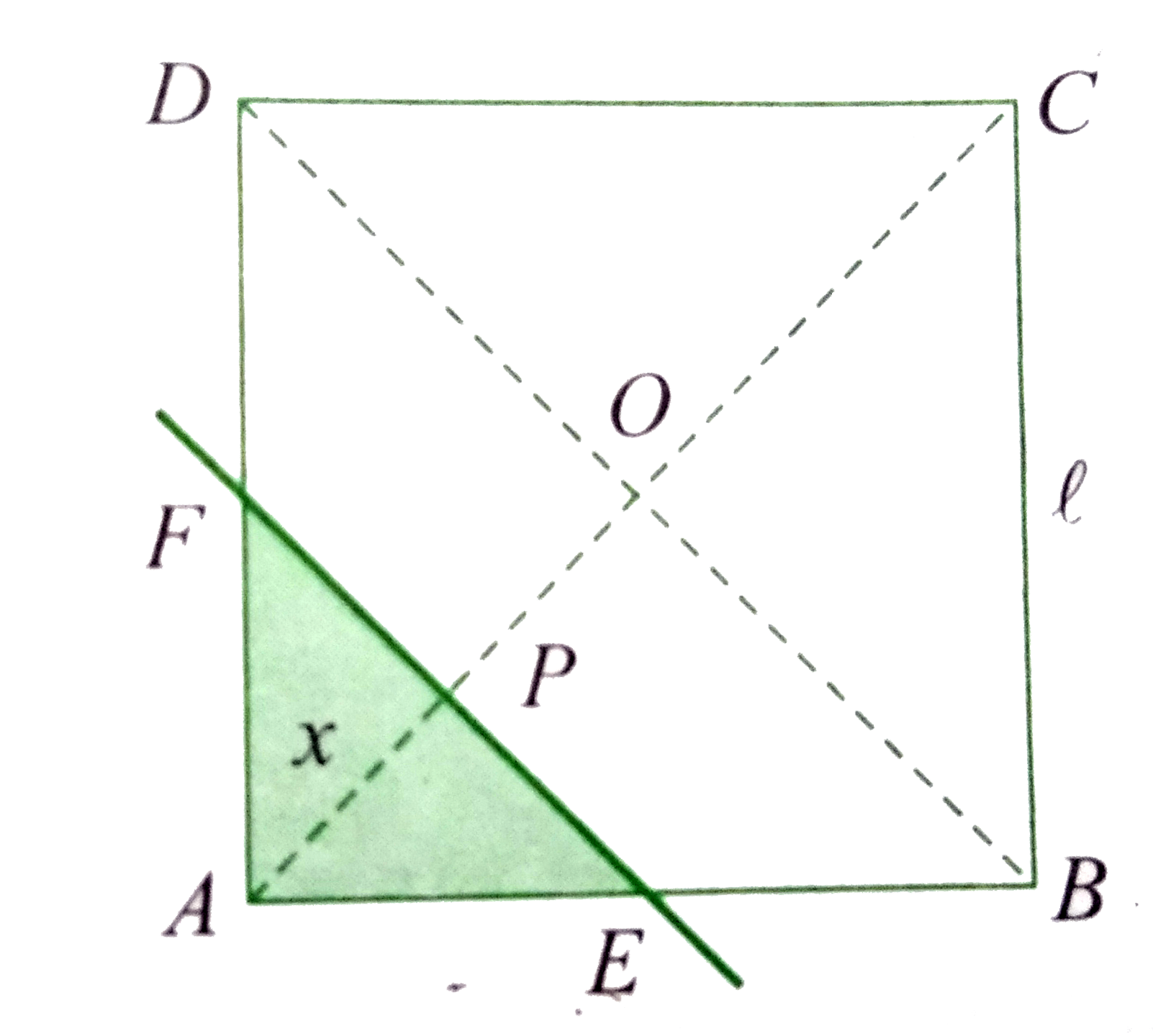
Case-II : when ` x=AP gt OA, i.e., x gt (l)/(sqrt(2)) " but " x le sqrt(2) l`

`ar(ABEFDA)=ar(ABCD)-ar( triangle CFE)`
`=l^(2)-(1)/(2)(sqrt(2)l-x)*2(sqrt(2)l-x) " " [ :' CP=sqrt(2)l-x]`
`=l^(2)-(2l^(2)+x^(2)-2sqrt(2)lx)=2sqrt(2)lx-x^(2)-l^(2)`
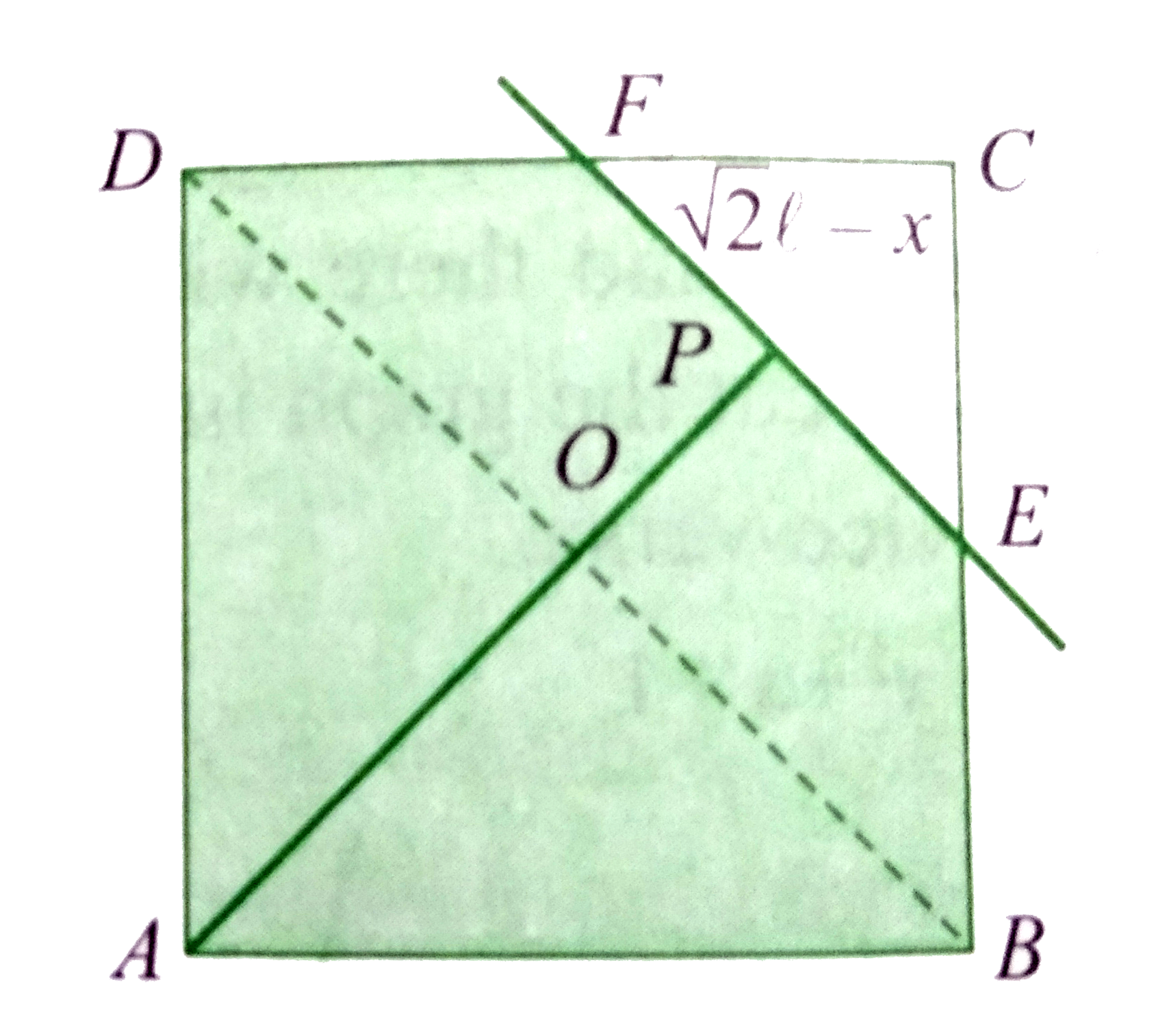
So, the required function s(x) is
`s(x) ={(x^(2)", "0le x le (l)/(sqrt(2))),(2sqrt(2)lx-x^(2)-l^(2)","(l)/(sqrt(2)) lt x le sqrt(2)l):}`
` :. s(x) ={((1)/(2)" at " x=(1)/(sqrt(2))),(8(sqrt(2)-l)" at " x=2):}`