ABCD is a square of side a. A line parallel to the diagonal BD at a distance x from the vertex A cuts the two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x.
To solve the problem, we need to find the area of the segment of the square with vertex A, given that a line parallel to the diagonal BD cuts the two adjacent sides at a distance x from vertex A.
1. Draw the Square:
- Let’s start by drawing square ABCD with vertices A, B, C, and D. Each side of the square has a length of 'a'.
2. Identify the Diagonal:
- The diagonal BD divides the square into two equal triangles. We will focus on the diagonal BD and the line parallel to it.
3. Draw the Line Parallel to BD:
- From vertex A, draw a line parallel to diagonal BD at a distance x. This line will intersect the sides AB and AD of the square.
4. Determine the Intersection Points:
- Let the line intersect side AB at point E and side AD at point F.
5. Identify the Angles:
- Since the line is parallel to diagonal BD, the angles formed at points E and F will be 45 degrees (because the diagonal BD makes a 45-degree angle with both sides AB and AD).
6. Calculate the Lengths:
- The distance from point A to point E (along AB) will be equal to x, and the distance from point A to point F (along AD) will also be equal to x.
- The length of the segment EF (the base of the triangle AEF) can be calculated using the properties of the triangle formed. Since the angles are 45 degrees, the length of EF will be 2x.
7. Calculate the Area of Triangle AEF:
- The area of triangle AEF can be calculated using the formula for the area of a triangle:
Area=12×base×height
- Here, the base is EF (which is 2x) and the height is the distance from A to the line EF (which is also x).
- Therefore, the area of triangle AEF is:
Area=12×2x×x=x2
8. Calculate the Area of the Segment:
- Since triangle AEF is formed by the line parallel to BD, the area of the segment of the square with vertex A is twice the area of triangle AEF (because there are two such triangles formed in the square).
- Thus, the area of the segment is:
Area of segment=2×x2=2x2
Final Answer:
The area of the segment of the square with vertex A, as a function of x, is:
Area=2x2
- Let’s start by drawing square ABCD with vertices A, B, C, and D. Each side of the square has a length of 'a'.
- The diagonal BD divides the square into two equal triangles. We will focus on the diagonal BD and the line parallel to it.
- From vertex A, draw a line parallel to diagonal BD at a distance x. This line will intersect the sides AB and AD of the square.
- Let the line intersect side AB at point E and side AD at point F.
- Since the line is parallel to diagonal BD, the angles formed at points E and F will be 45 degrees (because the diagonal BD makes a 45-degree angle with both sides AB and AD).
- The distance from point A to point E (along AB) will be equal to x, and the distance from point A to point F (along AD) will also be equal to x.
- The length of the segment EF (the base of the triangle AEF) can be calculated using the properties of the triangle formed. Since the angles are 45 degrees, the length of EF will be 2x.
- The area of triangle AEF can be calculated using the formula for the area of a triangle:
Area=12×base×height
- Here, the base is EF (which is 2x) and the height is the distance from A to the line EF (which is also x).
- Therefore, the area of triangle AEF is:
Area=12×2x×x=x2
- Since triangle AEF is formed by the line parallel to BD, the area of the segment of the square with vertex A is twice the area of triangle AEF (because there are two such triangles formed in the square).
- Thus, the area of the segment is:
Area of segment=2×x2=2x2
The area of the segment of the square with vertex A, as a function of x, is:
Area=2x2
Topper's Solved these Questions
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 1
5 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 2
6 Videos
- ESSENTIAL MATHEMATICAL TOOLS BOOK - ARIHANT MATHS ENGLISHCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
Similar Questions
ABCD is a square of side l. A line parallel to the diagonal BD at a distance 'x' from the vertex A cuts two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x. Find this area at x=1/√2 and at x=2, when l=2.
View SolutionProve that in any parallelogram the sum of squares of the diagonals is twice the sum of the squares of two adjascent sides. Also show that the difference of the squares on two adjacent sides is equal to the rectangle contained by either diagonal and the projection of the other upon it.
View Solution
Knowledge Check
ABCD is a square and one of its sides AB is also a chord of the circle as shown in the figure. What is the area of the square?
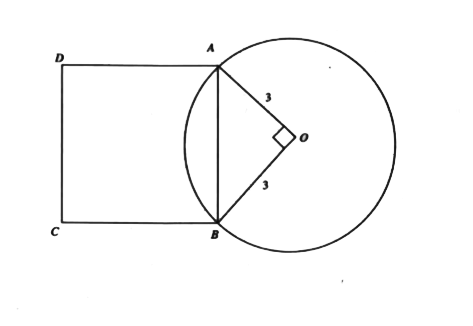 A3B9C12D18
A3B9C12D18
If one vertex of a square whose diagonals intersect at the origin is 3(cosθ+isinθ) , then find the two adjacent vertices.
View SolutionIf one of the sides of a square is 3x-4y-12 = 0 and the center is (0,0), then find the equations of the diagonals of the square.
View SolutionIf one of the sides of a square is 3x−4y−12=0 and the center is (0,0) , then find the equations of the diagonals of the square.
View SolutionFigure, ABCD is a square of side 2a. Find the ratio between the circumferences and the areas of the incircle and the circum-circle of the square.
View SolutionIf one diagonal of a square is along the line x=2y and one of its vertex is (3,0), then its sides through the vertex are given by the equations -
View SolutionA rhombus has two of its sides parallel to the lines y=2x+3andy=7x+2. If the diagonals cut at (1, 2) and one vertex is on the y-axis, find the possible values of the coordinate of that vertex.
View SolutionIf (a, b) be an end of a diagonal of a square and the other diagonal has the equation x−y=a, then another vertex of the square can be
View Solution
