Find the area bounded by y=1x2−2x+2 and x-axis.
Video Solution
Text Solution
y=1(x−1)2+1
When x=1,ymax .1
When x→±∞,y→0
Therefore, x-axis is the asymptote.
Also f(1+x)=f(1−x)
Hence, the graph is symmetrical about line x = 1
From these information the graph of function is as shown in the figure.
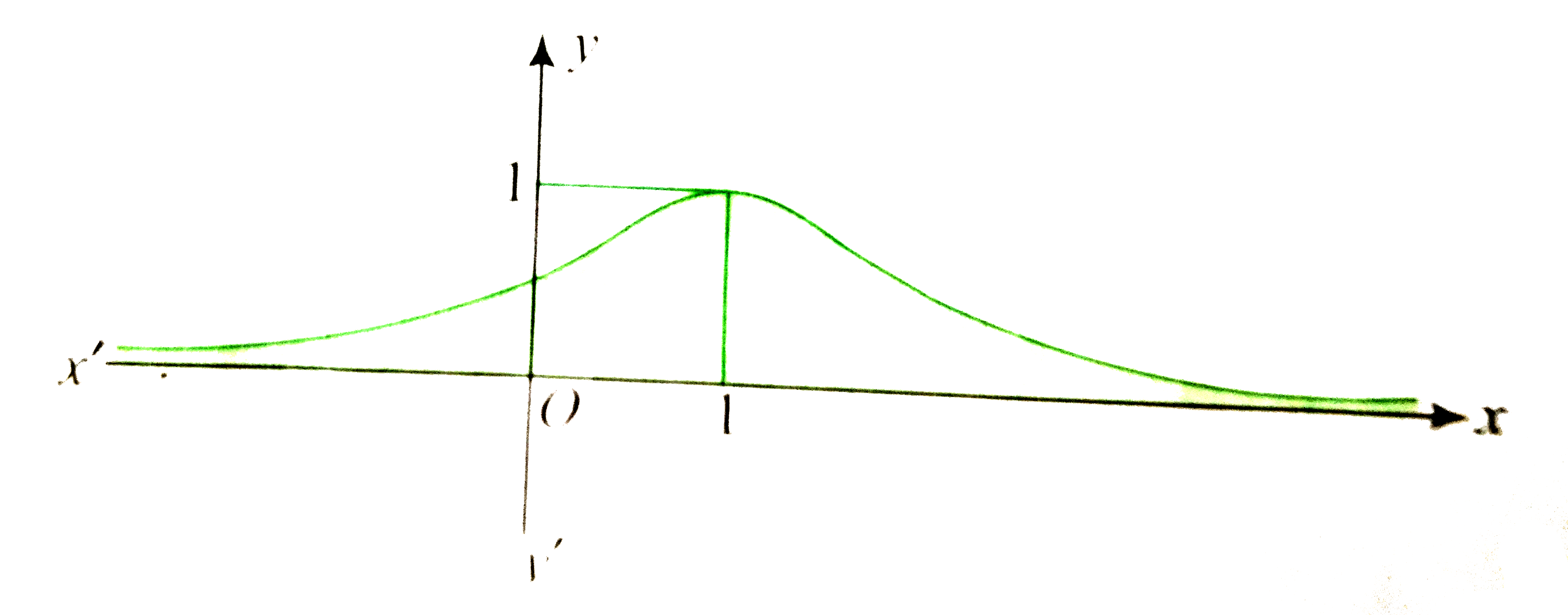
Area =2∞∫11(x−1)2+1dx=[2tan−1(x−1)]∞1=π sq. units.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.19videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.214videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank29videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank20videos
AREA UNDER CURVES
Similar Questions
Knowledge Check
- Question 1 - Select One
The area bounded by y=−x2+1 and the x-axis is
A13B23C43D83
Find the area bounded by y=1+2sin2x,X-axis,X=0 and x=π.
View SolutionFind the area bounded by y=x2 ,the x−axis and the lines x=−1 and x=1.
View SolutionFind the area bounded by y=x2, the x− axis and the lines x=−1andx=1
View SolutionFind the area bounded by the curve y=xex2 , x-axis and the ordinates x=0 and x=h.
View Solution(i) Find the area bounded by y=3x+2, the x-axis and the ordinates x=−2andx=1.
(ii) Find the area bounded by y=x, the x-axis and the line x=−1andx=2.View SolutionFind the area bounded by the curve y=−3|x|+2 and x-axis
View SolutionFind the area bounded by y=2x+1, the x-axis and x=0 and x=3.
View Solution

