Find the area bounded by the curve $y = (x - 1) (x - 2) (x - 3)$ lying between the ordinates $x = 0 a n d x = 3 .$

Video Solution

Text Solution

Verified by Experts

$y = f (x) = (x - 1) (x - 2) (x - 3)$
$y = 0, then x = 1, 2, 3 .$
So, graph of the function is as shown in the following figure.

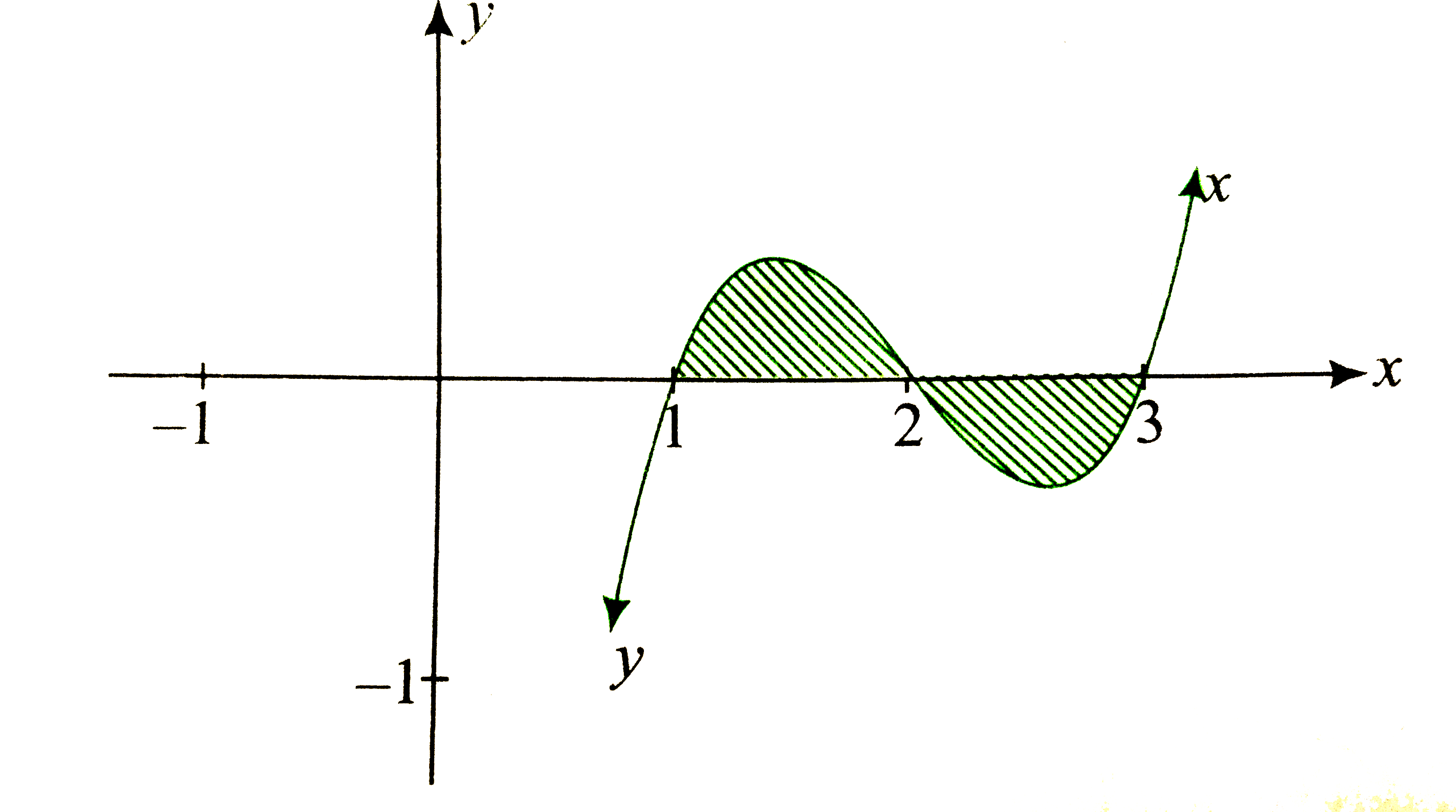
$Since f (2 - x) = - f (2 + x)$
$2 \int 1 f (x) d x = ∣ ∣ ∣ ∣ 3 \int 2 f (x) d x ∣ ∣ ∣ ∣$
$∴ Area of the shaded region,$
$A = 2 2 \int 1 f (x^{3} - 6 x^{2} + 11 x - 6) d x$
$= 2 {[\frac{x^{4}}{4} - 2 x^{3} + \frac{11 x^{2}}{2} - 6 x]}_{1}^{3}$
$= 2 \times \frac{1}{4} = \frac{1}{2}$

Updated on:21/07/2023