Find the area of the figure enclosed by the curve $5 x^{2} + 6 x y + 2 y^{2} + 7 x + 6 y + 6 = 0 .$

Video Solution

Text Solution

Verified by Experts

Equation of curve can be re-written as
$2 y^{2} + 6 (1 + x) y + 5 x^{2} + 7 x + 6 = 0$
$\Rightarrow y_{1} = \frac{- 3 (1 + x) - \sqrt{(3 - x) (x - 1)}}{2}$
$y_{2} = \frac{- (1 + x) + \sqrt{(3 - x) (x - 1)}}{2}$
Therefore, the curves $(y_{1} and y_{2})$ are defined for values of x for whih $(3 - x) (x - 1) \geq 0,$ i.e., $1 \leq x \leq 3 .$
(Actually the given equation represents an ellipse, because $Δ \neq 0 and h^{2} < a b .$ )

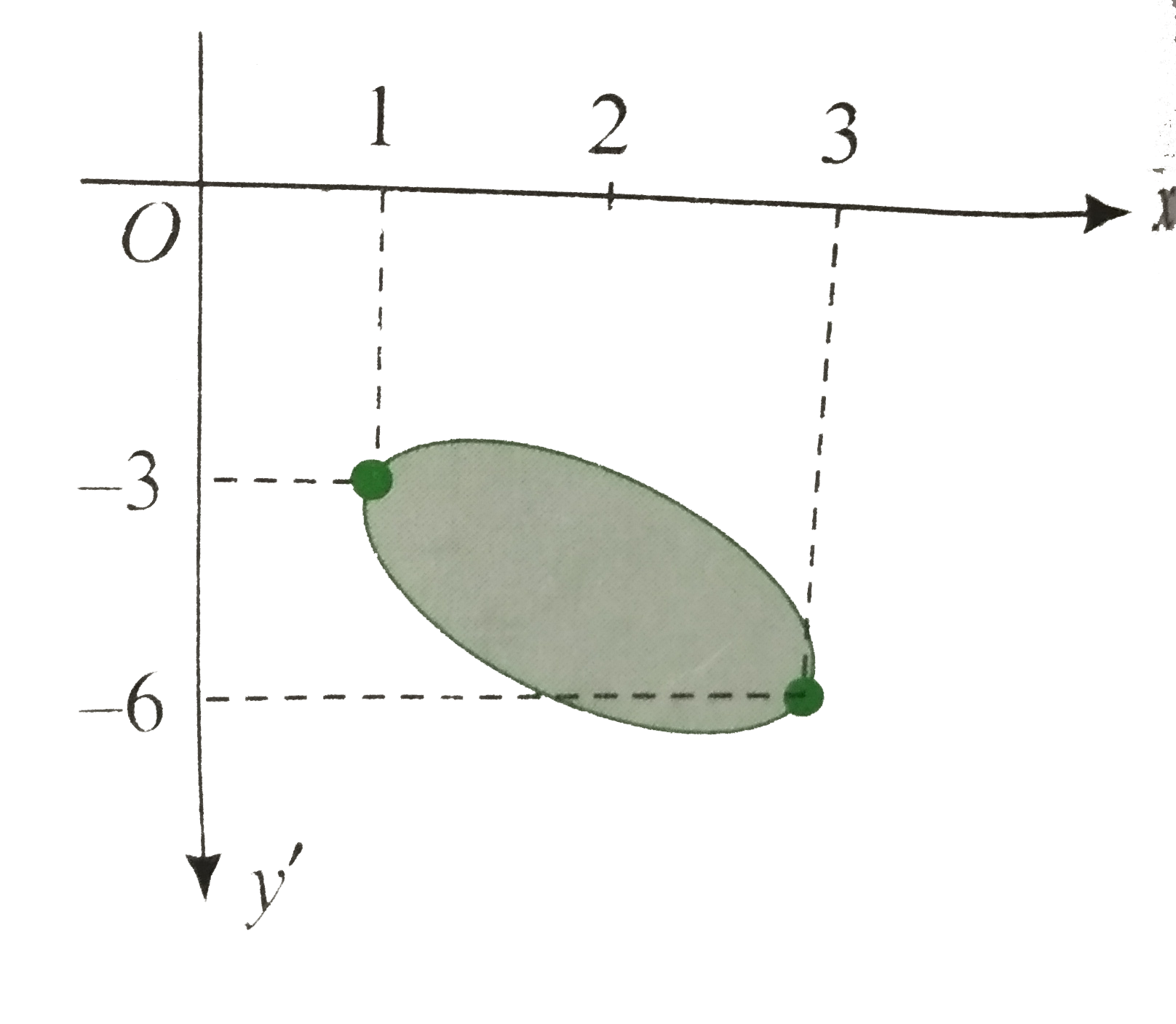
Required are will be given by
$A = 3 \int 1 | y_{1} - y_{2} | d x \Rightarrow A = 3 \int 1 \sqrt{(3 - x) (x - 1)} d x$
$Put x = 3 {cos}^{2} θ + {sin}^{2} θ, i . e ., d x = - 2 sin 2 θ d θ$
$∴ A = 2 π / 2 \int 0 {sin}^{2} 2 θ d θ = \frac{π}{2}$ sq. units.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area above the x-axis enclosed by the curves $x^{2} - y^{2} = 0 and x^{2} + y - 2 = 0$ is
A $\frac{5}{3}$
B $\frac{7}{3}$
C $\frac{8}{3}$
D $\frac{10}{3}$

CENGAGE-AREA-Comprehension Type

Home
Ask Doubt
Profile