Find the area of the region bounded by the curve C:y=tanx,tan≥ntdrawn→C at x=π4, and the x-axis.
Video Solution
Text Solution
The given curve is y=tanx (1)
When x=π/4,y=1
i.e., co-ordinates of P are (π/4,1)
∴ equation of tangent at P is y−1=(sec2π4)(x−π/4)
or y=2x+1−π/2
The graphs of (1) and (2) are as shown in the figure.
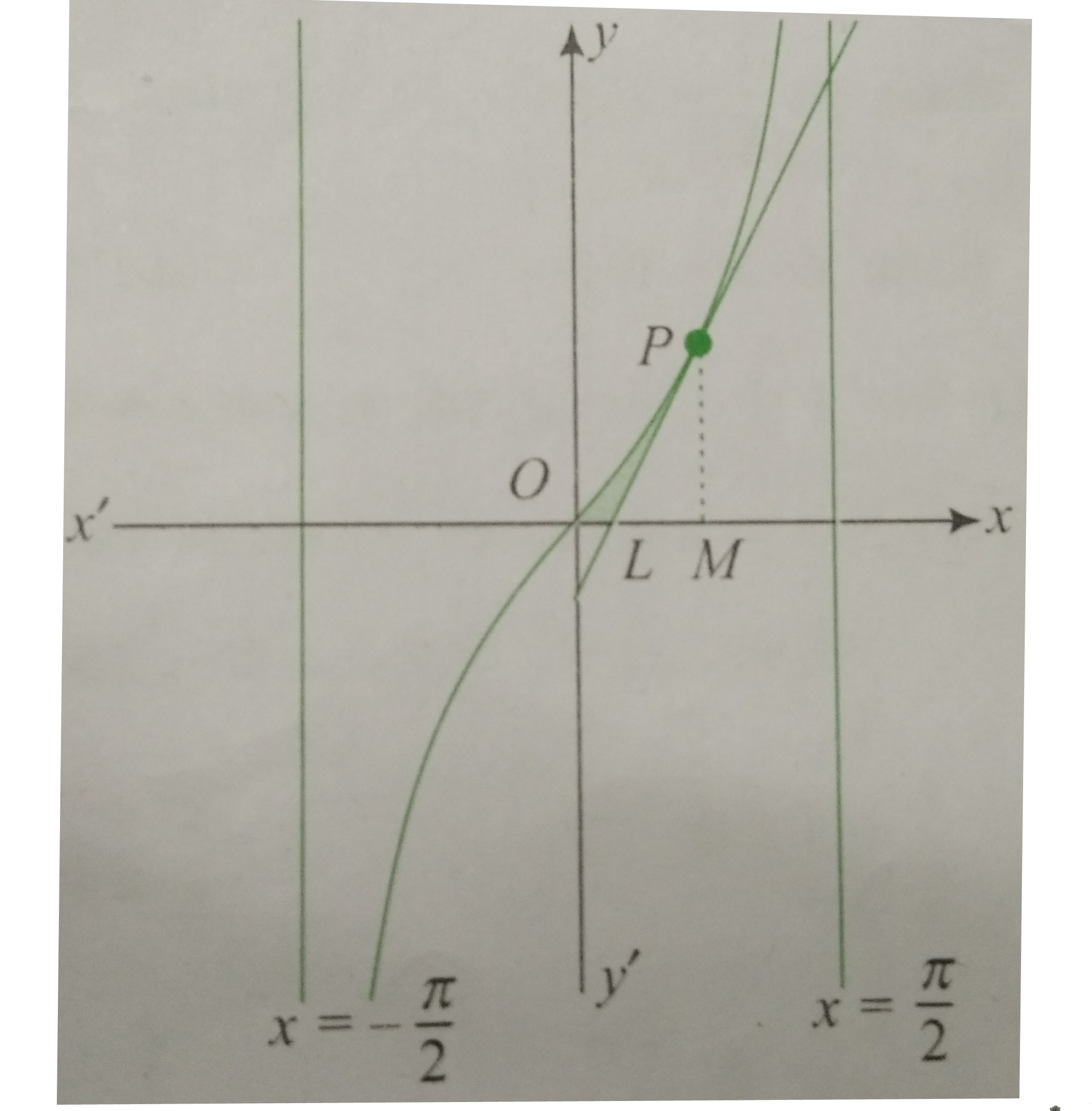
Tangent (2) meets x-axis at L(π−24,0)
Now, Required area =Shaded area
=Area OPMO−Ar(ΔPLM)
=∫π/40tanxdx−12(OM−OL)PM
=[logsecx]π/40−12×{π2−π−24}×1
=(1)/(2)[ log 2 -(1)/(2)]sq. units.
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
Find the area of the region bounded by the curve y2=4x and x2=4y.
A157 sq unitsB167 sq unitsC163 sq unitsD16 sq unitsArea of the region bounded by the curve y=tanx and lines y = 0 and x = 1 is
A∫10and(1−x)dxBtan1−∫tan10tan−1ydyC∫tan10tan−1ydyD∫10tan−1xdx
The area of the region bounded by the curve y=tanx, tangent drawn to the curve at x=π4 and the x-axis is
View SolutionArea of the region bounded by the curve y = tan x, tangent drawn to the curve at x =π4 and the x-axis is
View SolutionFind the area of the region bounded by the curves y2=4ax and x2=4ay.
View SolutionFind the area of the region bounded by the curve y2=4x and x2=4y.
View SolutionFind the area of the region bounded by the curve y=sinx between x=0andx=2π.
View SolutionArea of the region bounded by the curves y=4,y=√x and x=−√y is
View Solution
