A curve is given by $b y y = {(\sqrt{4 - x^{2}}), 0 \leq x < 1 \sqrt{(3 x)}, 1 \leq x \leq 3 .$ Find the area lying between the curve and x-axis.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{1}{6} (2 π - \sqrt{3} + 36)$ sq. units

The given curve is
$y = {\begin{matrix} \sqrt{(4 - x^{2})}, & 0 \leq x < 1 \sqrt{(3 x)}, & 1 \leq x \leq 3 \end{matrix}$
Obviously, the curve is the are of the circle $x^{2} + y^{2} = 4 (1)$
between $0 \leq x < 1$ and the are of parabola $y^{2} = 3 x (2)$
between $1 \leq x \leq 3$
Required area = shaded area
=Area OABCO+Area CBDEC
$= ∣ ∣ ∣ \int_{0}^{1} \sqrt{(4 - x^{2})} d x ∣ ∣ ∣ + ∣ ∣ ∣ \int_{1}^{3} \sqrt{3 x} d x ∣ ∣ ∣$
$∣ ∣ ∣ {[\frac{1}{2} x \sqrt{(4 - x^{2})} + \frac{4}{2} {sin}^{- 1} (\frac{x}{2})]}_{0}^{1} ∣ ∣ ∣ + ∣ ∣ ∣ \sqrt{3} {[\frac{2}{3} x^{3 / 2}]}_{1}^{3 / 2} ∣ ∣ ∣$
$= (\frac{\sqrt{3}}{2} + \frac{π}{3}) + \frac{2}{3} (9 - \sqrt{3})$
$= \frac{1}{6} (2 π - \sqrt{3} + 36)$ sq. units.

|

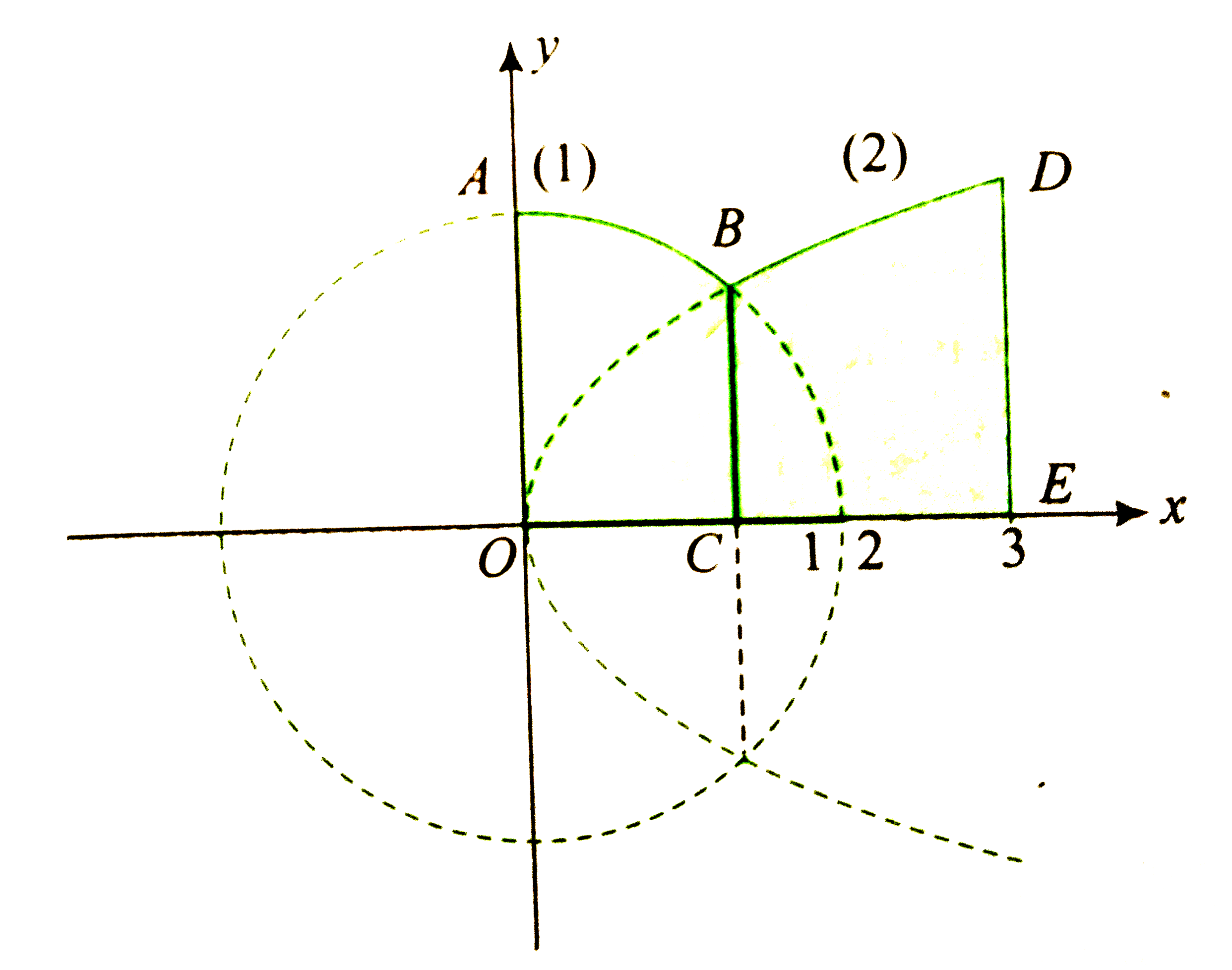
Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Area under the curve $y = \sqrt{16 - x^{2}}$ between x = 0 and x = 4 in the first quadrant is
A $8 π$
B $16 π$
C $4 π$
D $\frac{8 π}{3}$
Question 2 - Select One
The angle between the curves $y = sin x and y = cos x, 0 < x < \frac{x}{2}$ , is
A ${tan}^{- 1} (2 \sqrt{2})$
B ${tan}^{- 1} (3 \sqrt{2})$
C ${tan}^{- 1} (3 \sqrt{3})$
D ${tan}^{- 1} (5 \sqrt{2})$
Question 3 - Select One
If $f (x)$ is continuous on [-2, 2], where $f (x) = ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ \begin{matrix} \frac{sin a x}{x} + 2, for - 2 \leq x < 0 3 x + 5, for 0 \leq x \leq 1 \sqrt{x^{2} + 8} - b, for 1 < x < 2 \end{matrix}$ , then $a + b =$
A-15
B0
C2
D-2

CENGAGE-AREA-Exercise 9.1

Home
Ask Doubt
Profile