Consider two regions
$R_{1} : points P are nearer to (1,0) than to x = - 1 .$
$R_{2} : Points P are nearer to (0,0) than to (8,0)$ Find the area of the region common to $R_{1} and R_{2} .$

Text Solution

Verified by Experts

The correct Answer is: $\frac{64}{3}$ sq. units

$R_{1} :$ points P(x,y) are nearer to (1,0) than to x=-1
$∴ \sqrt{{(x - 1)}^{2} + y^{2}} < | x + 1 |$
$\Rightarrow y^{2} < 4 x$
$\Rightarrow point P lie inside parabola y^{2} = 4 x$
$R_{2} :$ Points P(x,y) are nearer to (0,0) than to (8,0)
$∴ | x | < | x - 8 |$
$\Rightarrow x^{2} < x^{2} - 16 x + 64$
$\Rightarrow x < 4$
$\Rightarrow$ point P lie to the left side of line x=4
The area of common region of $R_{1} and R_{2}$ is area bounded by x=4 and $y^{2} = 4 x .$

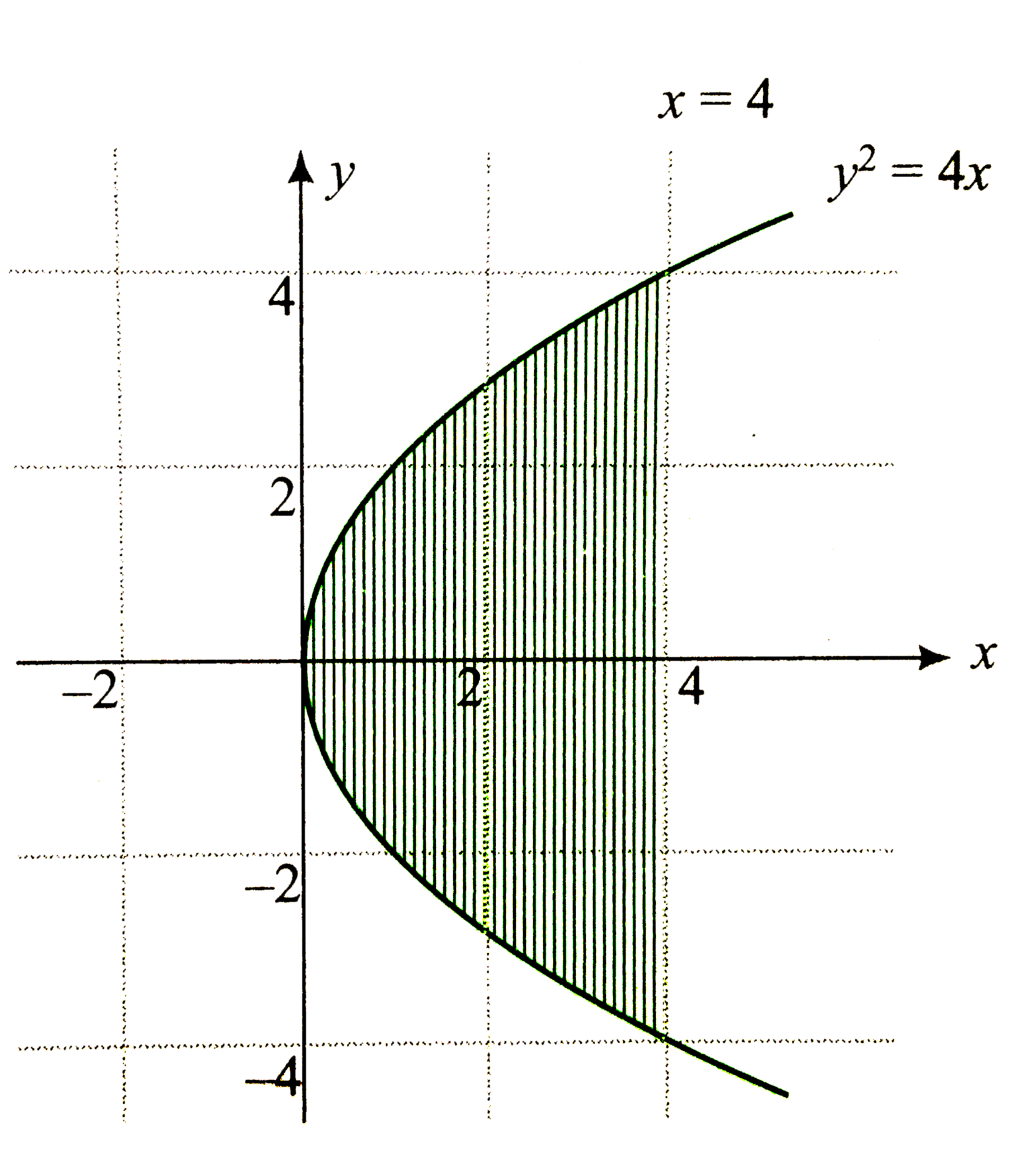
$∴ Required area = 2 4 \int 0 (4 - \frac{y^{2}}{4}) d y$ (Integrating along x-axis)
$= 2 {[4 y - \frac{y^{3}}{12}]}_{0}^{4}$
$= 2 [16 - \frac{64}{12}]$
$\frac{64}{3}$ sq. units

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The line x=0 divides the area enclosed by the curves
|x-1|-y=0.
|x|+y-3=0 into two areas $R_{1}$ and $R_{2}$ where $R_{1} < R_{2}$ Then the ratio of $R_{1} and R_{2}$ is
A $1 : 2$
B $1 : 4$
C $1 : \sqrt{2} + 1$
D $1 : 3$
Question 2 - Select One
Given a point $P (0, - 1, - 3)$ and the image of P in the plane $3 x - y + 4 z - 2 = 0$ is Q. Point R is $(3, - 1, - 2)$ find the area of $△ P Q R$
A $\frac{\sqrt{91}}{13}$
B $\frac{\sqrt{91}}{2}$
C $\sqrt{\frac{91}{2}}$
D $\sqrt{91}$

CENGAGE-AREA-Exercise 9.3

Home
Ask Doubt
Profile