The parabolas y2=4xandx2=4y divide the square region bounded by the lines x=4, y=4 and the coordinate axes. If S1,S2,S3 are the areas of these parts numbered from top to bottom, respectively, then
S1:S2≡1:1
S2:S3≡1:2
S1:S3≡1:1
S1:(S1+S2)=1:2
The correct Answer is:A, C, D
y2=4xandx2=4y meet at O(0,0)andA(4,4).
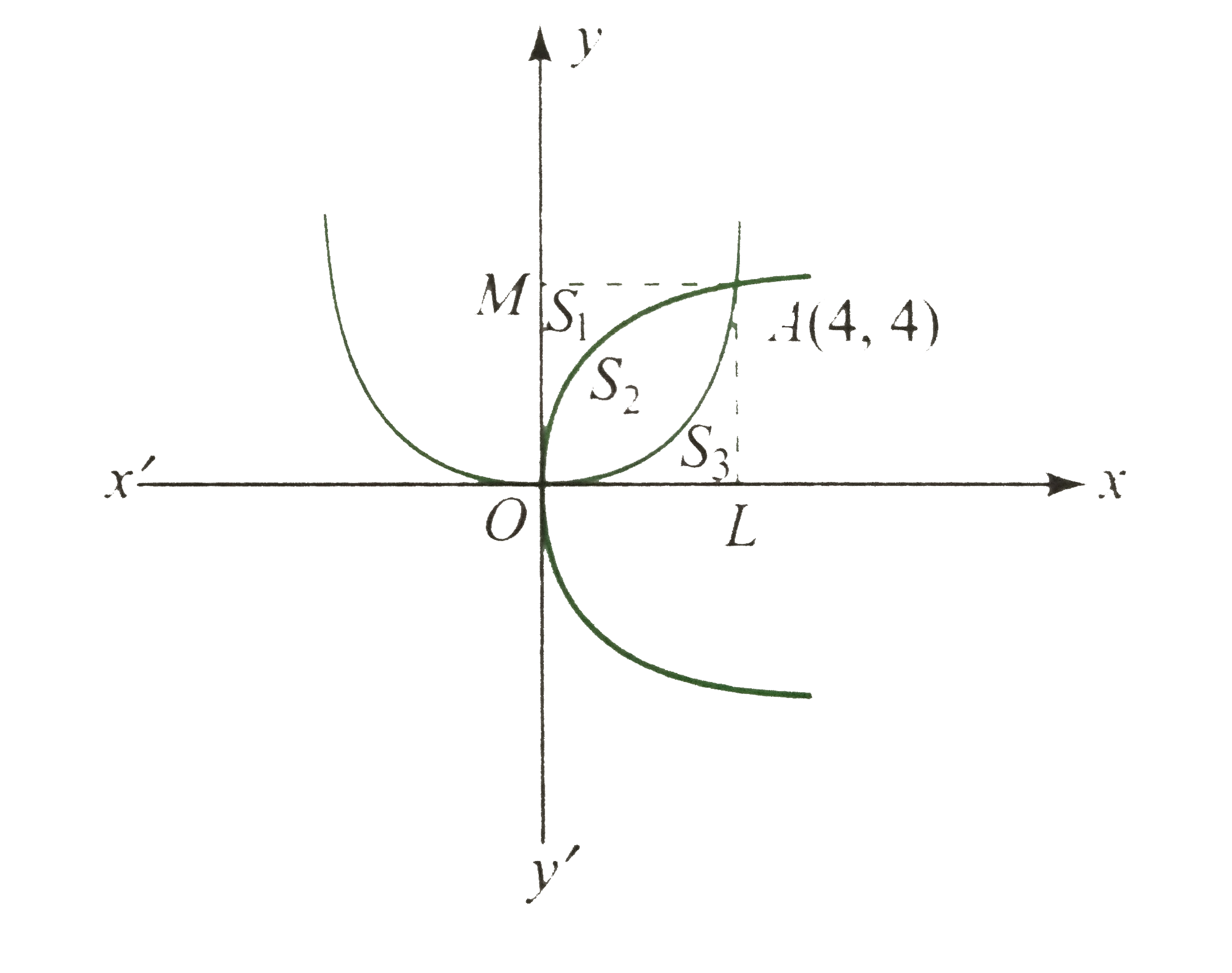
Now, S3=∫40x24dx=14[x33]40=112[64−0]=163.
S2=∫402√xdx−S3=2[x3/23/2]−163
=43[8−0]−163=163.
And S1=4×4−(S2+S3)=16−(163+163)=163.
Hence, S1:S2:S3=1:1:1
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)21videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)4videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Single)40videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank29videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank20videos
AREA UNDER CURVES
Similar Questions
The parabola x2=4y and y2=4x divide the square region bounded by the lines x=4, y=4 and the coordinate axes. If S1,S2,S3 are respectively the areas of these parts numbered from top to bottom, then S1:S2:S3 is (A) 2:1:2 (B) 1:2:1 (C) 1:2:3 (D) 1:1:1
View SolutionFind the area of the regions bounded by the parabola y2=4ax and the line x=a.
View Solution
Knowledge Check
- Question 1 - Select One
The parabola y2=4x and x2=4y divide the square region bounded by the lines x=4, y=4 and the coordinate axes. If S1,S2,S3 are respectively the areas of these parts numbered from top to bottom, then S1:S2:S3 is equal to
A1:1:1B2:1:2C1:2:3D1:2:1 - Question 2 - Select One
The parabolas y2=4xandx2=4y divide the square region bounded by the lines x=4, y=4 and the coordinate axes. If S1,S2,S3 are the areas of these parts numbered from top to bottom, respectively, then
A2:1:2B1:1:1C1:2:1D1:2:3 - Question 3 - Select One
The area of the region bounded by the lines y=2x+1y=3x+1 and x=4 is
A16 sq unitB1213 sq unitC1216 sq unitD8 sq unit
Find the area of the region bounded by the parabola x2=4y\ and the line x=4y−2
View SolutionFind the area of the region bounded by the parabola y2=4ax and the line x=a.
View SolutionFind the area of the region bounded by the parabola y2=2x and the line x−y=4
View SolutionProve that the curves y2=4x and x2=4y divide the area of square bounded by x=0,x=4,y=4 and y=0 into three equal parts.
View SolutionThe area of the region bounded by the parabola y2=4ax and the line y=mx is
View Solution

