Two curves C1≡[f(y)]2/3+[f(x)]1/3=0andC2≡[f(y)]2/3+[f(x)]2/3=12, satisfying the relation (x−y)f(x+y)−(x+y)f(x−y)=4xy(x2−y2)
The area bounded by C1andx+y+2=0 is
5/2 sq. units
7/2 sq. units
9/2 sq. units
None of these
The correct Answer is:C
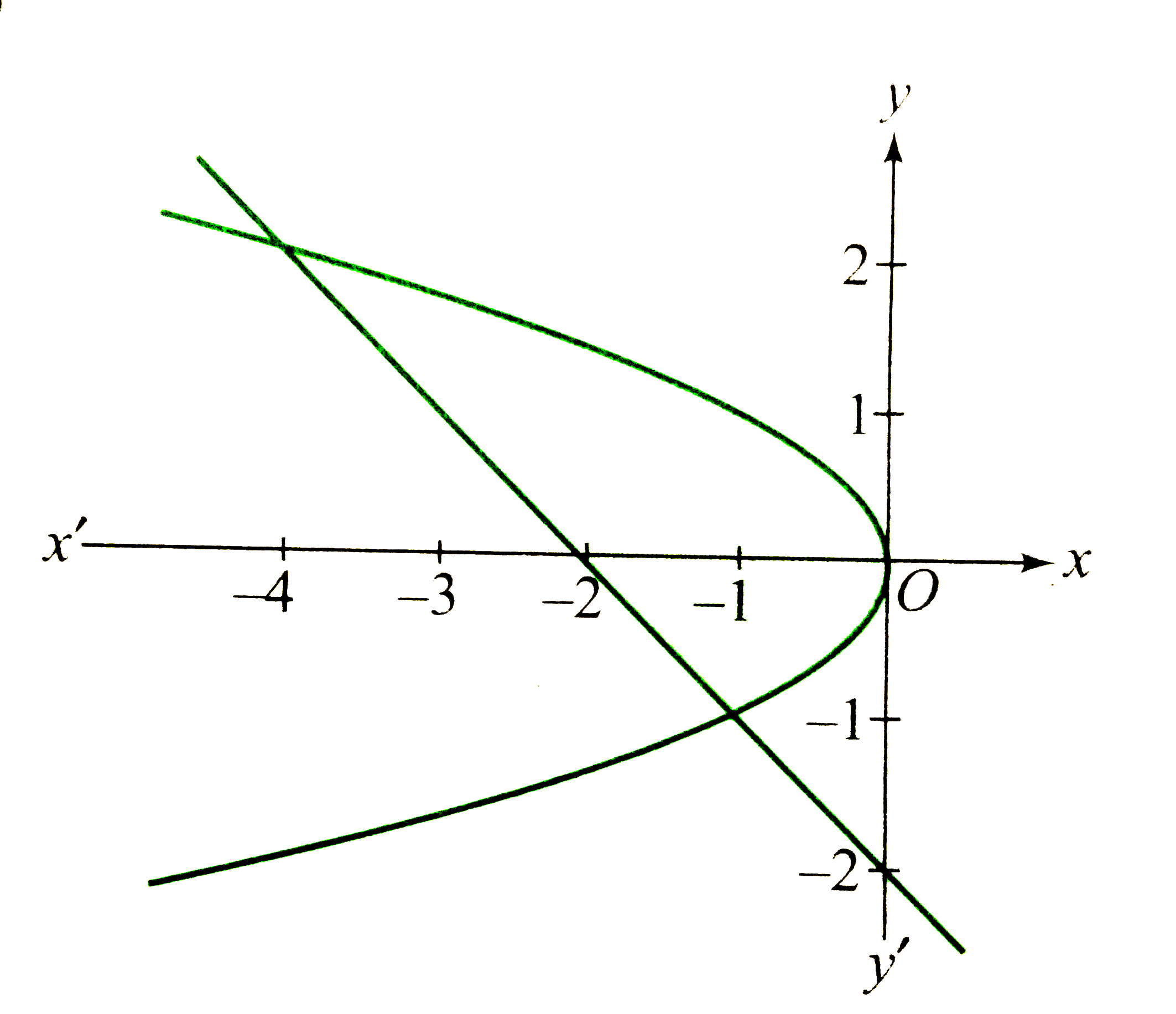
Required area =2∫−1(−y2−(−y−2))dy
=[y22+2y−y33]21
=[42+4−83−(12−2+13)]
=9/2 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)
4 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)
16 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Two curves C1≡[f(y)]2/3+[f(x)]1/3=0andC2≡[f(y)]2/3+[f(x)]2/3=12, satisfying the relation (x−y)f(x+y)−(x+y)f(x−y)=4xy(x2−y2)
The area bounded by the curve C2and|x|+|y|=√12 is
View SolutionTwo curves C1≡[f(y)]2/3+[f(x)]1/3=0andC2≡[f(y)]2/3+[f(x)]2/3=12, satisfying the relation (x−y)f(x+y)−(x+y)f(x−y)=4xy(x2−y2)
The area bounded by the curve C1andC2 is
View Solution
Knowledge Check
Two curves C1≡[f(y)]2/3+[f(x)]1/3=0andC2≡[f(y)]2/3+[f(x)]2/3=12, satisfying the relation (x−y)f(x+y)−(x+y)f(x−y)=4xy(x2−y2)
The area bounded by C1andC2 isA2π−√3 sq. unitsB2π+√3 sq. unitsCπ+√6 sq. unitsD2√3−π sq. unitsTwo curves C1≡[f(y)]2/3+[f(x)]1/3=0andC2≡[f(y)]2/3+[f(x)]2/3=12, satisfying the relation (x−y)f(x+y)−(x+y)f(x−y)=4xy(x2−y2)
The area bounded by the curve C2and|x|+|y|=√12 isA12π−24 sq. unitsB6−√12 sq. unitsC2√12−6 sq. unitsDNone of these
A curve Cis given by
(f(y))23+(f(x))13=0, satisfies, the equation
(x−y)f(x+y)−(x+y)f(x−y) Then =4xy(x2−y2).
area of the region bounded by curve C and the line a = -3, in sq. units, is A. Find A22.
View SolutionIf a function satisfies (x−y)f(x+y)−(x+y)f(x−y)=2(x2y−y3)∀x,y∈Randf(1)=2, then
View SolutionIf a function satisfies (x−y)f(x+y)−(x+y)f(x−y)=2(x2y−y3)∀x,y∈Randf(1)=2, then
View SolutionIf f(x,y)=2x2−xy+2y2 then find fx at the point (1,2)
View SolutionIf the function / satisfies the relation f(x+y)+f(x−y)=2f(x),f(y)∀x,y∈Randf(0)≠0 , then
View SolutionLet f(x) be a real valued function satisfying the relation f(xy)=f(x)−f(y) and limx→0f(1+x)x=3. The area bounded by the curve y=f(x), y-axis and the line y=3 is equal to
View Solution
