Doubtnut Promotions Sticky

Let f(x) be a continuous function fiven by f(x)={2x,|x|≤1x2+ax+b,|x|>1,then
If f(x) is continuous for all real x then the value of a2+b2 is

A

3

B

4

C

5

D

11

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

f(x)=⎧⎪⎨⎪⎩x2+ax+bx<−12x−1≤x≤1x2+ax+bx>1
∵ f(x)iscont∈uousatx=−1andx=1
∴ (−1)2+a(−1)+b=−2⇒b−a=−3 ...(1)
and 2=(1)2+a.1+b⇒a+b=1 ...(2)
Solving (1) and (2), we get a=2,b=−1
∴ f(x)=⎧⎪⎨⎪⎩x2+2x−1x<−12x−1≤x≤1x2+2x−1x>1
Given curves are y=f(x),x=−2y2and8x+1=0
Solving x=−2y2,y=x2+2x−1(x<−1) we get x=-2
Also, y=2x,x=−2y2 meet at (0,0)
y=2xandx=−1/8 meet at (−18,−14)
The required area is the shaded region in the figure
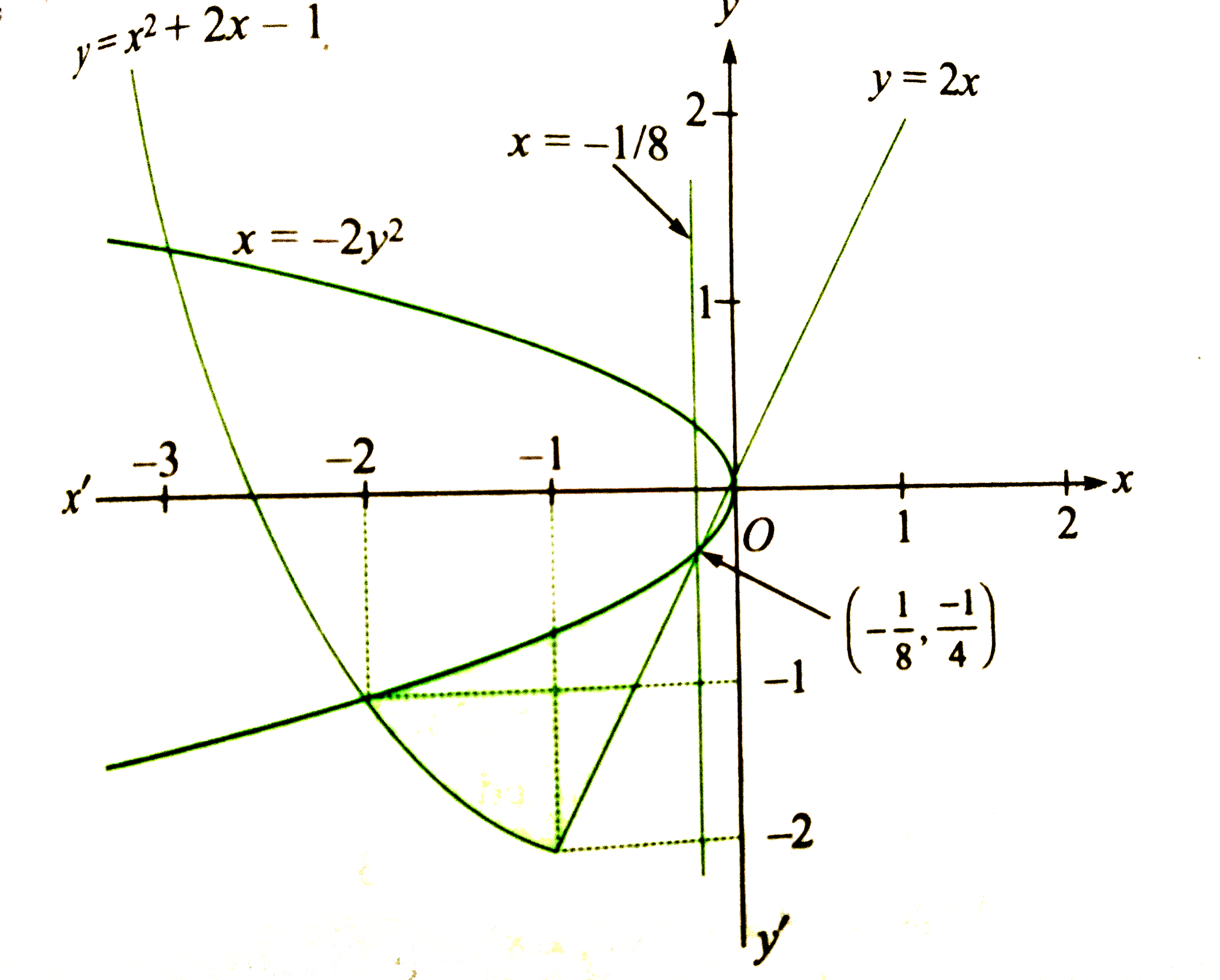
ocr_image
∴ Required area
=∫−1−2[−√−x2−(x2+2x−1)dx]+∫−1/8−1[−√−x2−2x]dx
=[1√22(−x)3/23−x33−x2+x]−1−2+[1√22(−x)3/23−x2]−1/8−1
=(√23+13−1−1)−(43+83−4−2)+(√23.116√2−164)−(√23−1)
=(√2−53)−(4+8−183)+(4−3192)−(√2−33)
=257192 sq. units

|
Updated on:21/07/2023
Class 12MATHSAPPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let f(x)={(x+a)x<1ax2+1x≥1 then f(x) is continuous at x =1 for

    Aa = 0
    Ba = 1
    CAll a∈R
    DNo value of a
  • Question 2 - Select One

    If f(x)={ax+3,x≤2a2x−1,x>2, then the values of a for which f is continuous for all x are

    Aa and -2
    B1 and 2
    C−1and2
    D−1and−2
  • Question 3 - Select One

    Let f(x)={1|x|for |x|≥1ax2+bfor |x|<1. If f(x) is continuous and differentiable everywhere, then

    Aa=12,b=−32
    Ba=−12,b=32
    Ca=1, b=-1
    Da=b=1