Find the minimum integral value of k for which the equation ex=kx2 has exactly three real distinct solutions.
Given equation is ex=kx2.
⇒k=exx2
Now let f(x)=exx2
∴f′(x)=(x−2)exx3
f′(x)=0∴x=2, which is the point of minima.
Also f(2)=e24
limx→∞exx2=∞ (using L' Hospital rule twice)
ex→∞xx2=0
limx→0exx2=∞
Further f(x)>0,∀x∈R.
From this information, the graph of f(x) is as shown in the following figure.
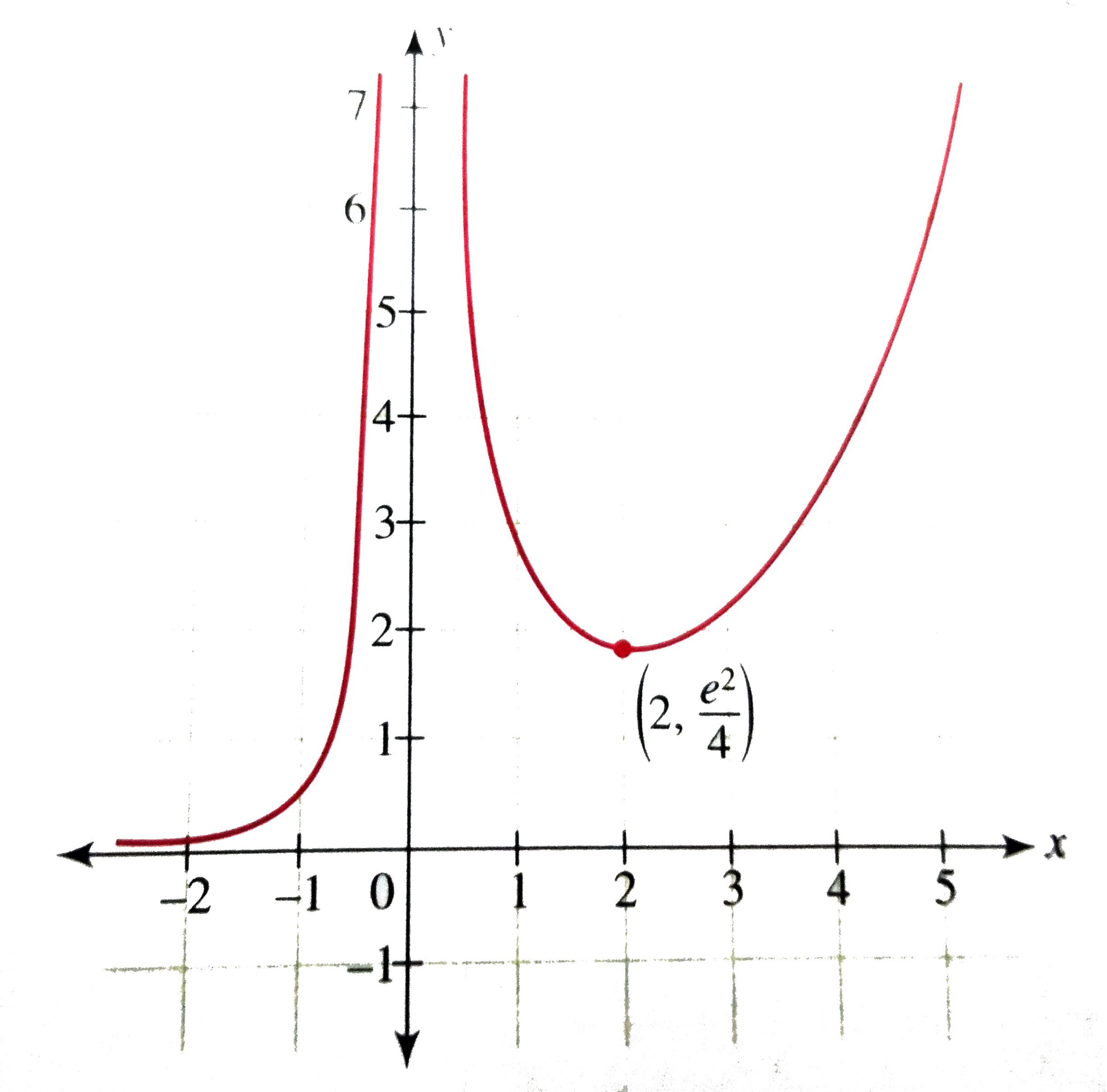
Thus, three real distinct solutions for k<e24,k∈I.
So, kmin=2.
Topper's Solved these Questions
Similar Questions
Number of integral values of b for which the equation x33−x=b has three distinct solutions is____
View SolutionNumber of integral values of b for which the equation x33−x=b has three distinct solutions is____
View SolutionNumber of integral values of b for which the equation x33−x=b has three distinct solutions is____
View SolutionNumber of integral values of k for which the equation 4cos−1(−|x|)=k has exactly two solutions, is:
View Solutionthe value(s) if k for which the equation 5kx2−8x+2=0 has real roots
View SolutionFind sum of all possible integral value (s) of 'p' for which the equation ∣∣∣x+1x−3∣∣∣=p−3 has exactly two distinct solutions.
View SolutionFind the least positive value of k for which the equation x2+kx+4=0 has real roots.
View SolutionFind the values of k for which the equation x2−4x+k=0 has distinct real roots.
View SolutionFind the values of k for which the equation x2+5kx+16=0 has no real roots.
View SolutionFind the value of K for which the quadratic equation kx2+2x+1=0,has real and distinct root.
View Solution
