Question

Draw the graph of the function $f\left(x\right)=x^x$

Explanation

We have `f(x)=x^(x)`
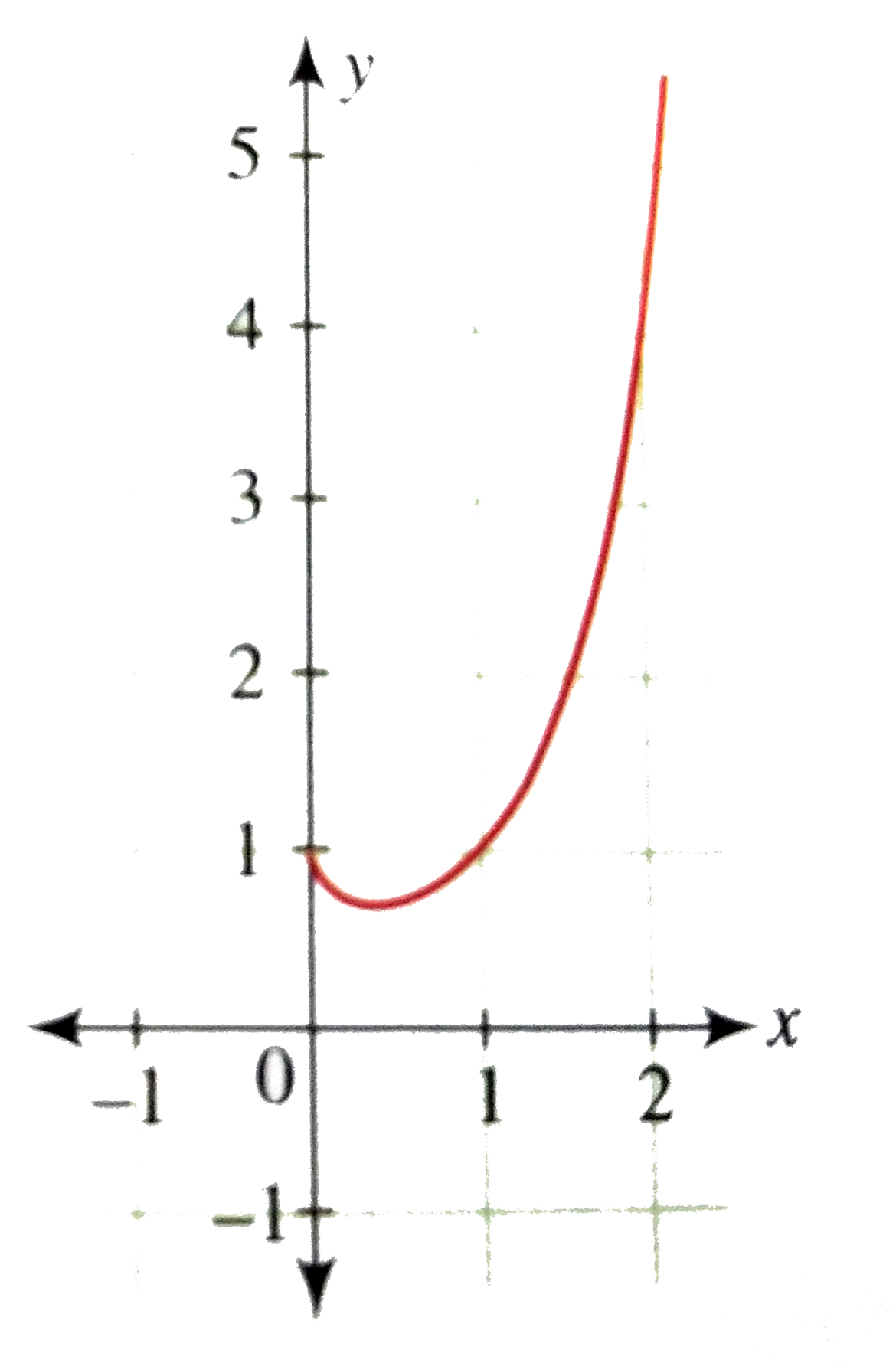
Clearly, the domain of the function is `x gt 0`.
Differentiating we get, `f^(')(x) = x^(x)(1+log_(e)x)`
Also for `x lt 1/e, f^(')(x) lt 0` and for `x gt 1//e, f^(')(x) lt 0`.
Thus, `x=1//e` is the point of minima.
`f(1//e) = (1//e)(1//e)`
Also, `lim_(x to 0) x^(x) =e^(lim_(x to 0)limxlogx) = e^(lim_(x to o)(1//x)/(-1//x^(2)))=e^(lim_(xto0)(-x))=e^(0)=1`
and `lim_(xtoinfty)x^(x)=infty`
From the above discussion, the graph of the function is as shown in the following figure.