Draw the graph of the function f(x)=2x2−loge|x|

Text Solution
Verified by Experts

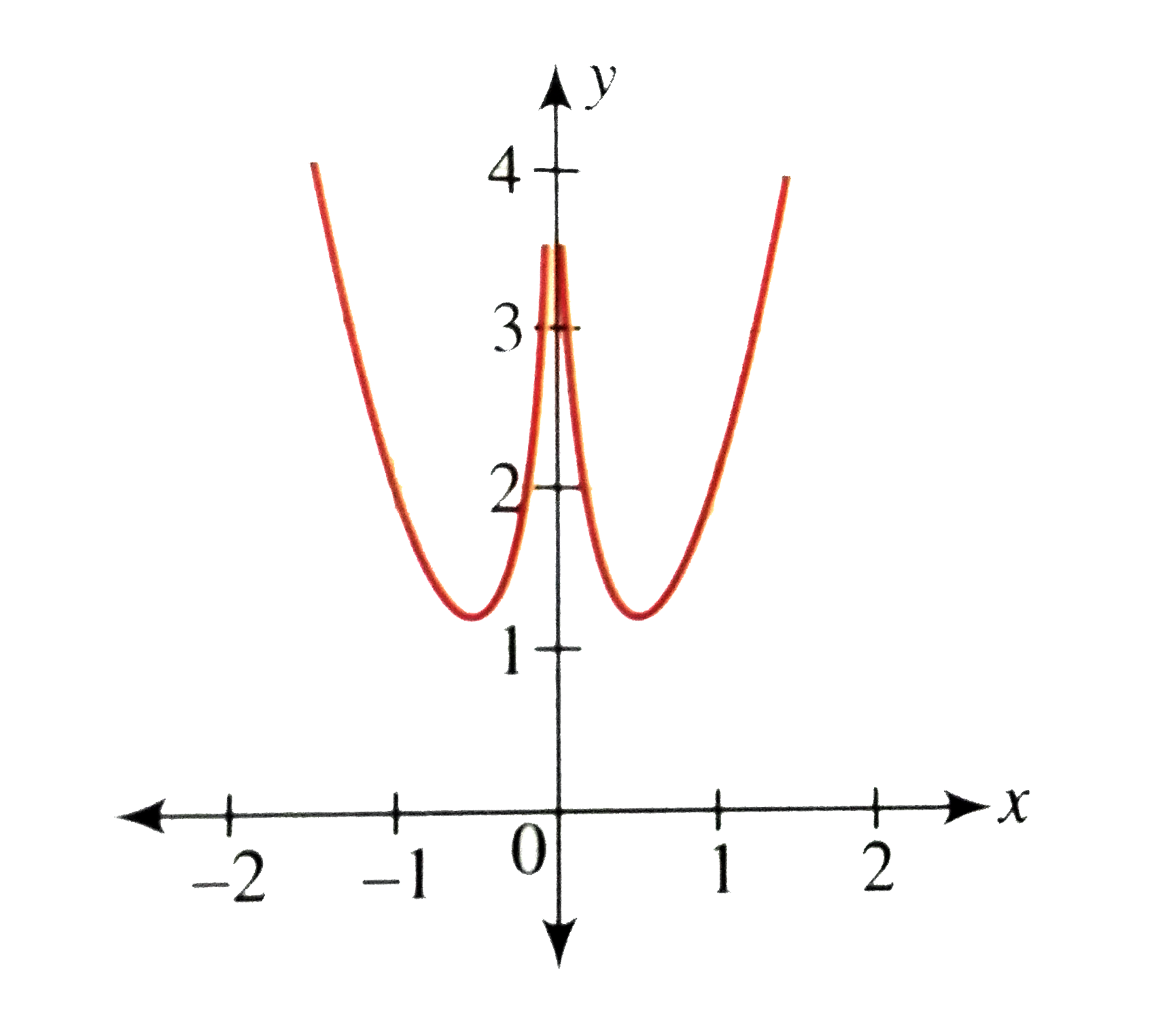
We have f(x)=2x2−loge|x|,x≠0
Clearly, f(x) is an even function, hence its graph is symmetrical about the y-axis.
limx→0+(2x2−loge|x|)=∞ and limx→±∞(2x2−loge|x|)=∞ (as difference between the value of 2x2 and ln|x| is infinite, loge|x| increases very slowly, but 2x2 increases faster)
Also f′(x)=4x−1x=4x2−1x
f′(x)=0⇒x=±12
From the limiting values of the function at x=0 and at inifinity, we can conclude that x=±12 are points of minima.
From the above discussion, the graph of the function is as shown in the following figure.
ocr_image

Doubtnut Promotions Banner
|