The locus of the foot of the perpendicular from the origin on each member of the family $(4 a + 3) x - (a + 1) y - (2 a + 1) = 0$

A

${(2 x - 1)}^{2} + 4 {(y + 1)}^{2} = 5$

B

${(2 x - 1)}^{2} + {(y + 1)}^{2} = 5$

C

${(2 x + 1)}^{2} + 4 {(y - 1)}^{2} = 5$

D

${(2 x - 1)}^{2} + 4 {(y - 1)}^{2} = 5$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Given family of lines is $(4 a + 3) x - (a + 1) y - (2 a + 1) = 0$
or $(3 x - y - 1) + a (4 x - y - 2) = 0$
Family of lines passes through the fixed point P which is the intersection of
$3 x - y = 1$ and $4 x - y = 2$
Solving we get $P (1, 2)$ .

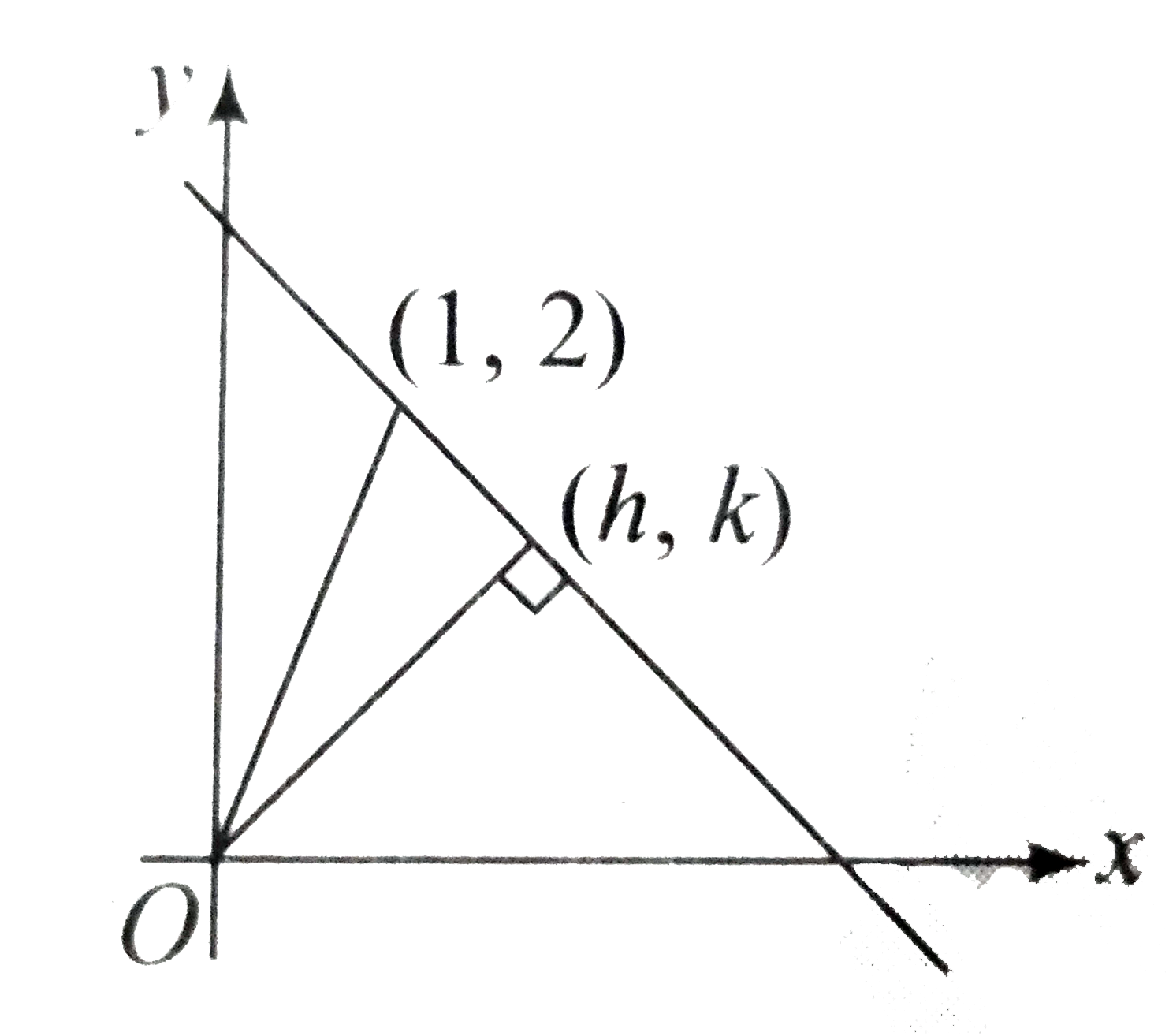
Now let (h,k) be the foot of perpendicular on each of the family.
$∴ \frac{k}{h} . \frac{k - 2}{h - 1} = - 1$
$∴$ Locus is $x (x - 1) + y (y - 2) = 0$
or ${(2 x - 1)}^{2} + 4 {(y - 1)}^{2} = 5$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The foot of the perpendicular drawn from the origin to the plane $x + y + z = 3$ is
A $(0, 1, 2)$
B $(0, 0, 3)$
C $(1, 1, 1)$
D $(- 1, 1, 3)$
Question 2 - Select One
The locus of the foot of the perpendicular drawn from the origin to any tangent to the hyperbola $\frac{x^{2}}{36} - \frac{y^{2}}{16} = 1$ is
A ${(x^{2} + y^{2})}^{2} = 36 x^{2} - 16 y^{2}$
B ${(x^{2} - y^{2})}^{2} = 36 x^{2} - 16 y^{2}$
C ${(x^{2} + y^{2})}^{2} = 36 x^{2} + 16 y^{2}$
D ${(x^{2} - y^{2})}^{2} = 36 x^{2} + 16 y^{2}$
Question 3 - Select One
The locus of the of perpendicular from (1,2) on each member of the family of lines
$(1 + 2 t) x + (1 - t) y + t - 1 = 0, t \in R$ is
A $x^{2} + y^{2} + x - 3 y + 2 = 0$
B $x^{2} + y^{2} - x - 3 y + 2 = 0$
C $x^{2} + y^{2} - x - 3 y - 4 = 0$
DNone of these

CENGAGE-STRAIGHT LINE-Multiple Correct Answers Type

Home
Ask Doubt
Profile