Let A,B,C,D be collinear points in that order. Suppose AB:CD=3:2andBC:AD=1:5. Then AC:BD is(A) 1:1 (B)11:10 (C) 16:11 (D) 17:13
A
1:1
B
11:10
C
16:11
D
17:13
Video Solution
Text Solution
The correct Answer is:A
|
Answer
Step by step video, text & image solution for Let A,B,C,D be collinear points in that order. Suppose AB: CD = 3:2 and BC : AD = 1:5. Then AC :BD is(A) 1:1 (B) 11:10 (C) 16:11 (D) 17:13 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If A:B=2:3 , B:C = 4:5, C:D = 6:7. then A : B : C : D is-
A18:24:30:35B16:24:30:35C16:22:30:35DNone of these - Question 2 - Select One
If A:B = 3:4 and B:C= 6:5 then A:(A+C) is:
A. 9:11
B. 9:10
C. 9:19
D. 6:7ADBBCADC - Question 3 - Select One
(2) If A:B=2:3,B:C=4:5 and C:D=6:7, find A:D
A0.088194444444444B0.29722222222222C0.69097222222222D0.17569444444444
A, B, C, D are four consecutive points on a circle such that AB=CD. Prove that AC=BD
View SolutionIn Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
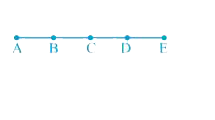
AD = AC + ___________View Solution(2) If A:B=2:3,B:C=4:5 and C:D=6:7, find A:D
View SolutionIn Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
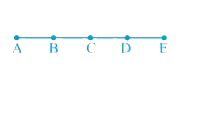
AE = ________ × AB.View SolutionA,B,C,D are any four points, prove that →AB.→CD+→BC.→AD+→CA.→BD=0.
View Solution