The axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the right without friction and with speed v1. It passes over the cylinder to the dashed position. Whe it first makes contact with the cylinder, it slips on the cylinder, but the friction is large enough so that slipping ceases before M loses contact with the cylinder. The cylinder has a radius R and a rotational inertia I.
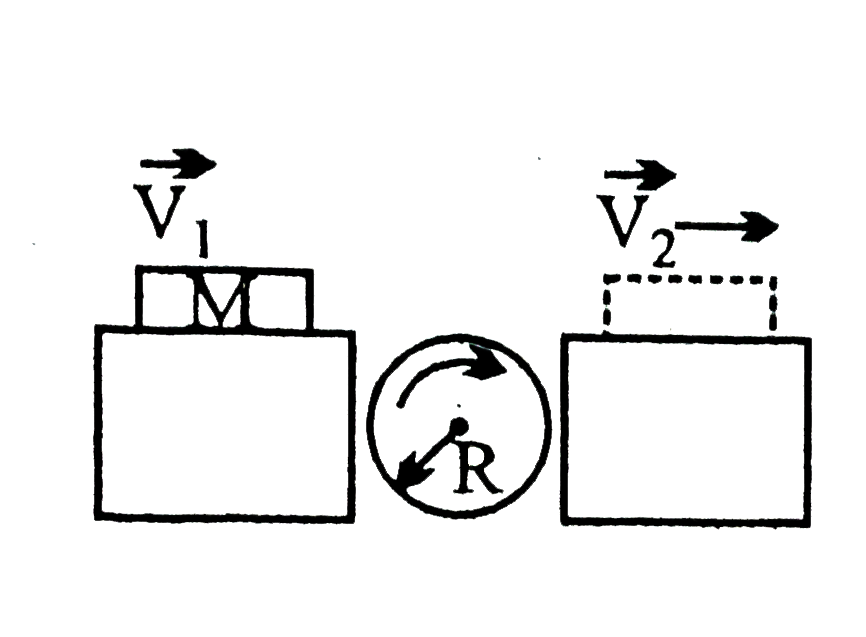
Ouestion given below consists of two statements each printed as (I) and (II), while answering the question you are required to choose any one of the following four responses on the basis of above situation
I. Momentum of the block-cylinder system is conserved.
II. Force of friction between blockk and cylinder is internal force of block-cylinder system.
if both (I) and (II) are true and (II) is the correct explanation of (I)
if both (I) and (II) are true but (II) is not correct explanation of (I)
if (I) is true but (II) is false
if (I) is false and (II) is true
The correct Answer is:A
Assertion is false as hinge applier some force on the block cylinder system
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Physics, SECTION-1 (PART-A) [MULTIPLE CORRECT CHOICE TYPE]
5 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Physics, SECTION-1 (PART-B) [MATRIX TYPE]
2 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Physics, SECTION-1 (PART-A)
5 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
The axis of a cylinder of radius R and moment of inertia about its axis I is fixed at centre O as shown in figure - 5.73 . Its highest point A is in level with two plane horizontal surfaces . A block of mass M is initially moving to the right without friction with speed v1 . It passes over the cylinder to the dotted position . calculate the speed v2 in the dotted position and the angular velocity acquired by the cylinder . if at the time of detaching from cylinder block stops slipping on it .
⎡⎢ ⎢⎣v11+IMR2,v1R(1+IMR2)⎤⎥ ⎥⎦

View SolutionA clockwise torque of 6N−m is applied to the circular cylinder as shown in the figure. There is no friction between the cylinder and the block.

View Solution
Knowledge Check
The axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v1. It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I
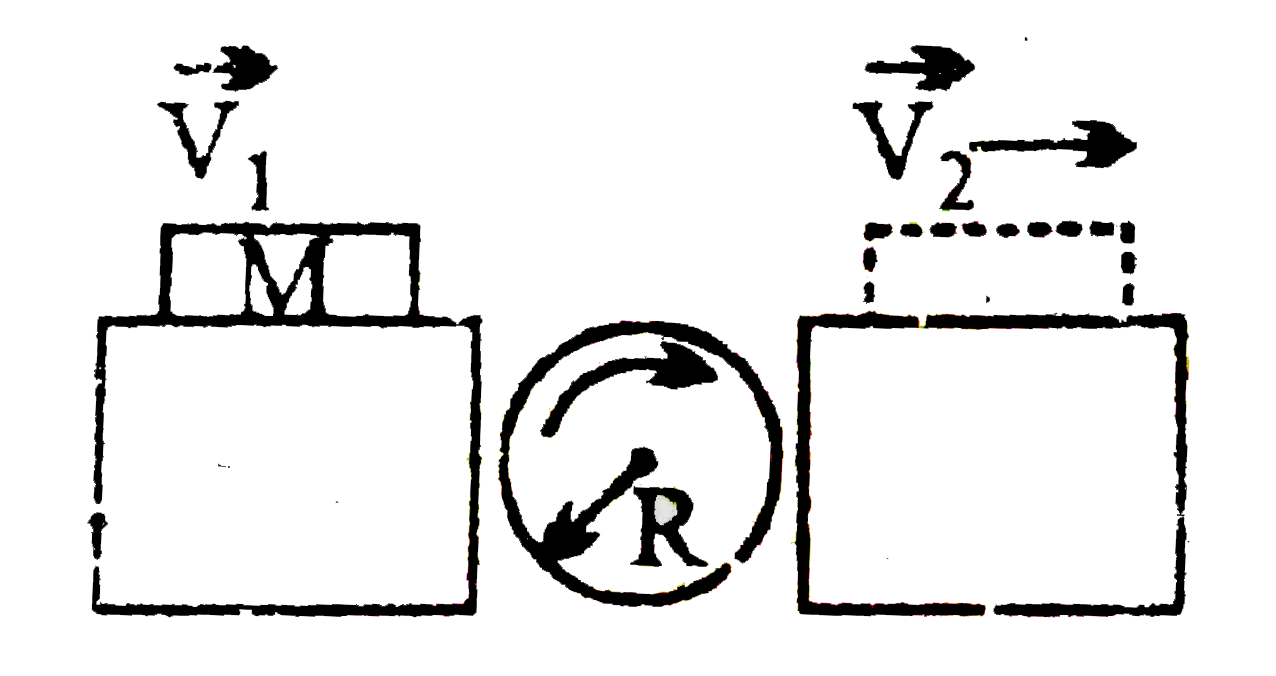
If ω is final angular velocity of the cylinder, thenAv1=ωRBv2=ωRCv1<ωRDnoneThe axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v1. It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I

For the entire process the quantitiy (ies) which will remain conserved for the (cylinder+block) system is/ are (anuglar momentum is considered about the cylinder axis)Amechanical energy, momentum and angular momentumBmechanical energy & angular momentum onlyCmomentum & angular momentum onlyDangular momentum onlyThe axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v1. It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I

Assertion : Momentum of the block -cylinder system is conserved
Reason: Force of friction between block and cylinder is internal force of block -cylinder system.AIf both (A) and (R) are true and (R) is the correct explanation of (A)BIf both (A) and (R) are true but (R) is not correct explanationC(if (A) is true but (R) is falseDIF (A) is false and (R) is true
A uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is

View SolutionA uniform disc of mass M and radius R is initially at rest. Its axis is fixed through O. A block of mass m is moving with speed v1 on a frictionless surface passes over the disc to the dotted position. On coming in contact with the disc, it slips on it. The slipping ceases before the block loses contact with the disc, due to the high friction. Now, the velocity of mass m is
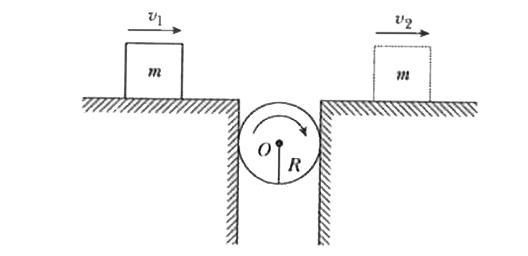
View SolutionA clockwise torque of 6N−m is applied to the circular cylinder as shown in the figure. There is no friction between the cylinder and the block.

View SolutionA uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is

View SolutionConsider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is Ffriction at point P? It is assumed that the cylinder does not slip.
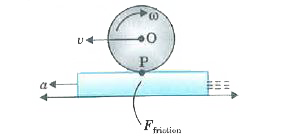
View Solution
