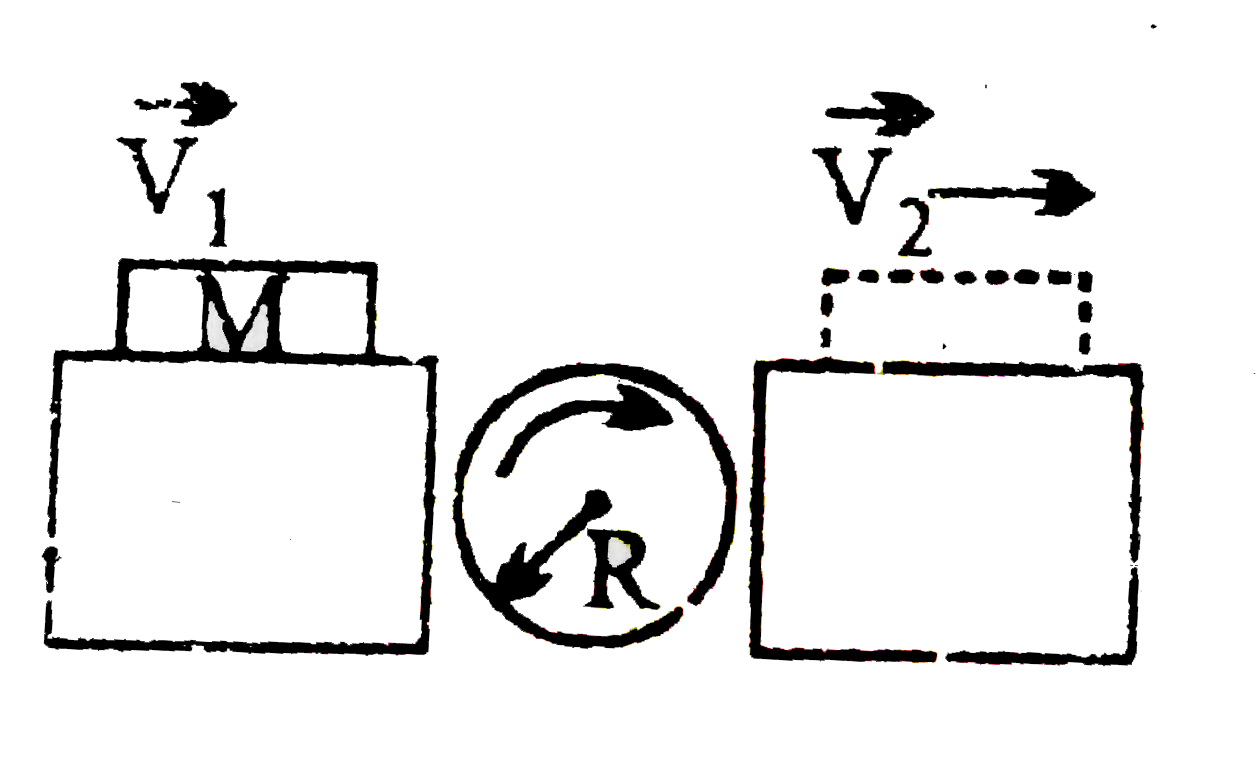
The axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the right without friction and with speed v1. It passes over the cylinder to the dashed position. Whe it first makes contact with the cylinder, it slips on the cylinder, but the friction is large enough so that slipping ceases before M loses contact with the cylinder. The cylinder has a radius R and a rotational inertia I.
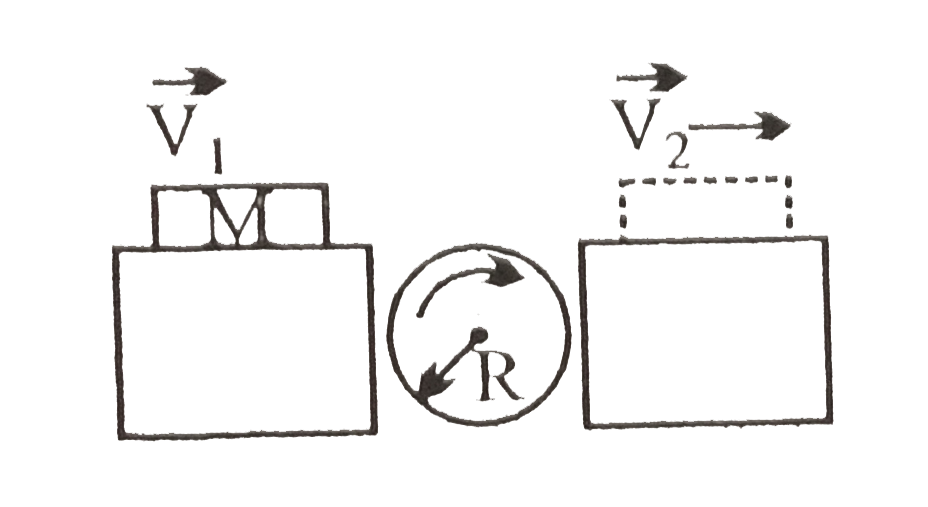
If w is final angular velocity of the cylinder, then
v1=ωR
v2=ωR
v1<ωR
none
The correct Answer is:A
As slipping ceases before M loses contact with cylinder v2=ωR
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Physics, SECTION-1 (PART-A) [MULTIPLE CORRECT CHOICE TYPE]
5 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Physics, SECTION-1 (PART-B) [MATRIX TYPE]
2 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Physics, SECTION-1 (PART-A)
5 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
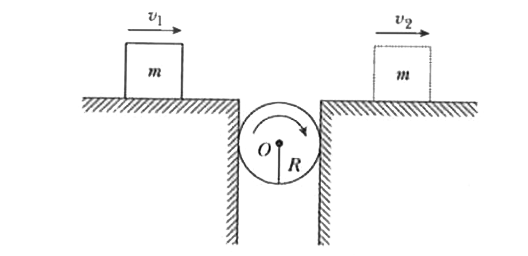
The axis of a cylinder of radius R and moment of inertia about its axis I is fixed at centre O as shown in figure - 5.73 . Its highest point A is in level with two plane horizontal surfaces . A block of mass M is initially moving to the right without friction with speed v1 . It passes over the cylinder to the dotted position . calculate the speed v2 in the dotted position and the angular velocity acquired by the cylinder . if at the time of detaching from cylinder block stops slipping on it .
⎡⎢ ⎢⎣v11+IMR2,v1R(1+IMR2)⎤⎥ ⎥⎦

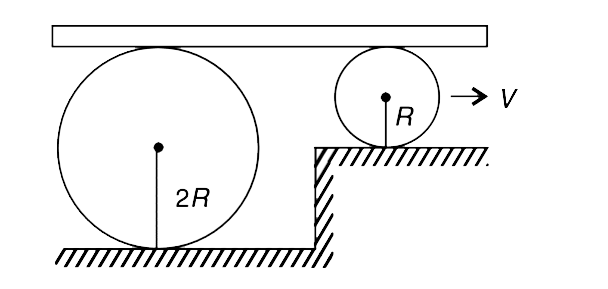
View SolutionIn the figure the plank resting on two cylinders is horizontal. The plank is pulled to the right such that the centre of smaller cylinder moves with a constant velocity v. Friction is large enough to prevent slipping at all surfaces. Find-
(a) The velocity of the centre of larger cylinder.
(b) The ratio of accelerations of the points of contact of the two cylinders with the plank.
View Solution
Knowledge Check
The axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v1. It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I
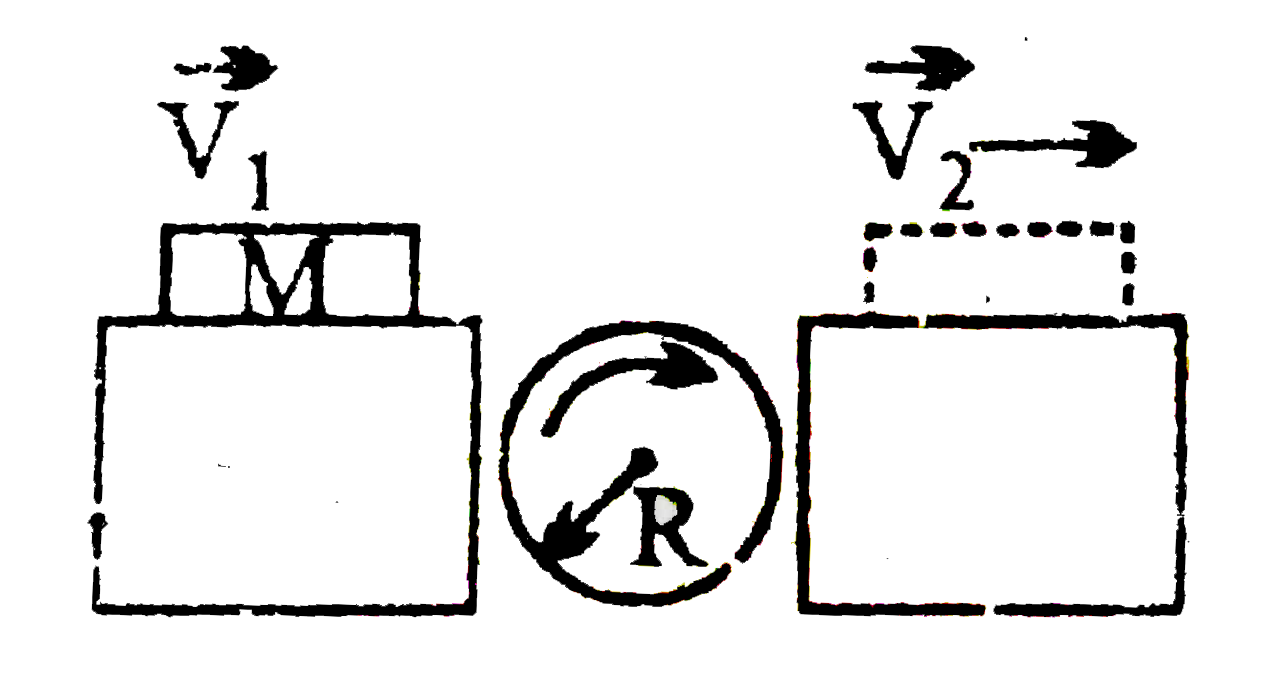
If ω is final angular velocity of the cylinder, thenAv1=ωRBv2=ωRCv1<ωRDnoneThe axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v1. It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I
Assertion : Momentum of the block -cylinder system is conserved
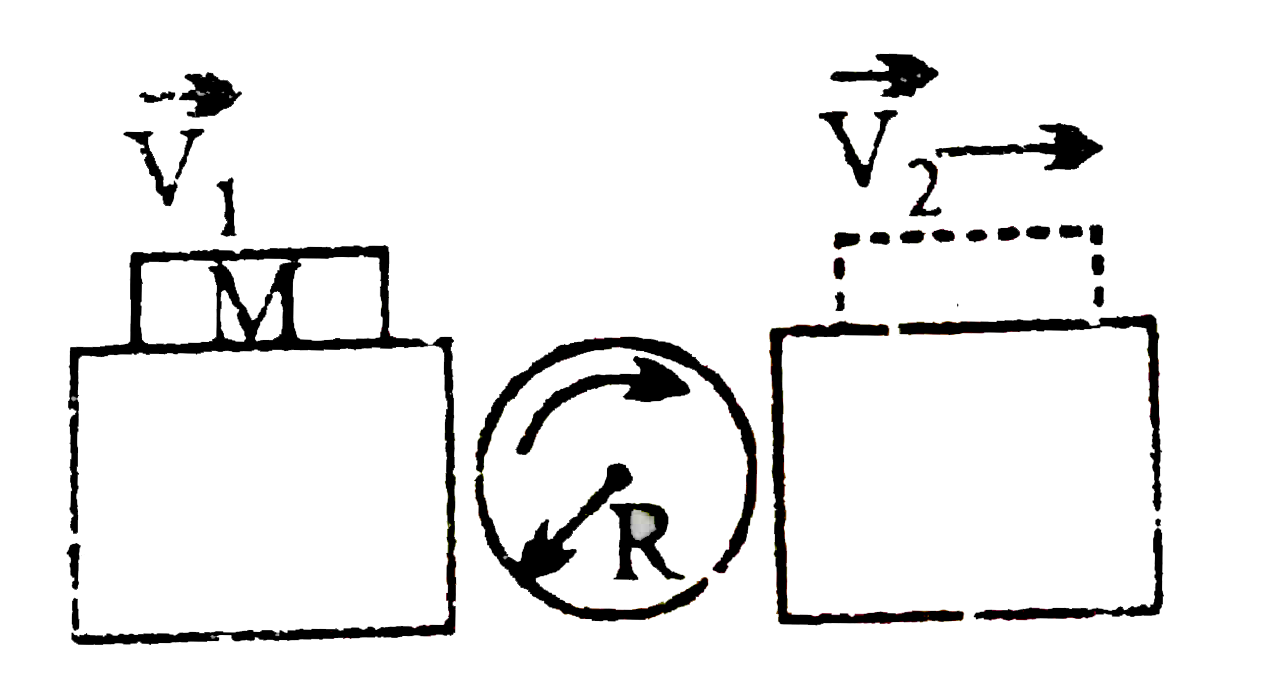
Reason: Force of friction between block and cylinder is internal force of block -cylinder system.AIf both (A) and (R) are true and (R) is the correct explanation of (A)BIf both (A) and (R) are true but (R) is not correct explanationC(if (A) is true but (R) is falseDIF (A) is false and (R) is trueThe axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v1. It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I
For the entire process the quantitiy (ies) which will remain conserved for the (cylinder+block) system is/ are (anuglar momentum is considered about the cylinder axis)Amechanical energy, momentum and angular momentumBmechanical energy & angular momentum onlyCmomentum & angular momentum onlyDangular momentum only
A rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radus R is placed horizontally at rest its length parallel to the edge such that the exis of the cylinder and the endg of the block are in the same vertical plane as shown in the figure below. Ther is sufficinet friction present at the edge s that a very small displacement causes the cylinder to roll off the edge without slipping. Determine:

(a) the angle θc through which the cylinder rotates before it leaves contact with the edge,
(b) the speed of the centre of mass of the cylinder before leaving contact with the edge, and
(c) the ratio of the translational to rotational kinetic energy of the cylinder when its centre of mass is in horizontal line with the edge.
View SolutionConsider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is Ffriction at point P ? It is assumed that the cylinder does not slip.
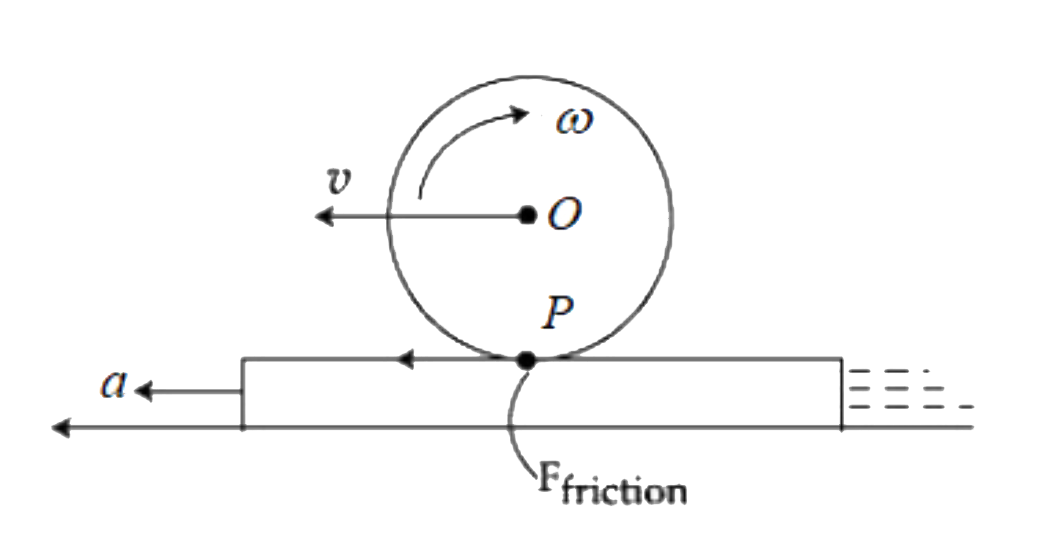
View SolutionConsider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is Ffriction at point P ? It is assumed that the cylinder does not slip.

View SolutionA uniform disc of mass M and radius R is initially at rest. Its axis is fixed through O. A block of mass m is moving with speed v1 on a frictionless surface passes over the disc to the dotted position. On coming in contact with the disc, it slips on it. The slipping ceases before the block loses contact with the disc, due to the high friction. Now, the velocity of mass m is
View SolutionConsider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is Ffriction at point P? It is assumed that the cylinder does not slip.
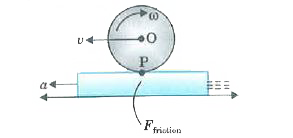
View Solution
