Fifteen sudents S1,S2,S3,….S15
participate in quiz competition. The number of ways in which they can be grouped into 5 teams of 3 each such that S1andS2 are in different teams is equal to
A
13!(3!)44!
B
14!(3!)44!
C
6(13!)(3!)44!
D
none
Video Solution
Text Solution
C
Required number of ways= (Number of ways in which 15 students can be divided in 5 teams )-( Number of ways when S1andS2 are in same group )
=15!(3!)55!−13C1×12!(3!)4⋅4!=15!(3!)55!−13!(3!)44!(15×143!×5−11)
13!(3!)44!(142−1)=6(13!)(3!)44!
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION-3 Part-A [ comprehension type ]3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION-3 Part-A [Reasoning type ]2videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY SECTION-2 Part-B ( Matrix type )2videos
TEST PAPERS
- BOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions1videos
PROBABILITY
- BOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column7videos
THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Sixteen players S1, S2, S3,…,S16 play in a tournament. Number of ways in which they can be grouped into eight pairs so that S1 and S2 are in different groups, is equal to
A(14)!26⋅6!B(15)!27⋅7!C(14)!27⋅6!D(14)!26⋅7! - Question 2 - Select One or More
S1 and S2 are two equipotential surfaces on which the potentials are not equal
AS1 and S2 cannot intersect.BS1 and S2 cannot both be plane surfaces.CIn the region between S1 and S2 the field is maximum where they are closest to each other.DA line of force from S1 and S2 must be perpendicular to both. - Question 3 - Select One
Light is falling on the surfaces S1,S2andS3 as shown below.

The surfaces on which the angle of incidence is equal to the angle of reflection areAS1andS3BAll the three surfacesCS1andS2DS2andS3
If S1={2},S2={3,6},S3={4,8,16},S4={5,10,20,40}....... then the sum of numbers in the set S15 is
View SolutionIf S1,S2,S3 are the sums of first n natural numbers, their squares and their cubes respectively then S3(1+8S1)=
View SolutionIf Sr denotes the sum of the first r terms of an A.P., then show that S3r−Sr−1S2r−S2r−1 is equals
View SolutionLight is falling on the surfaces S1,S2andS3 as shown below:
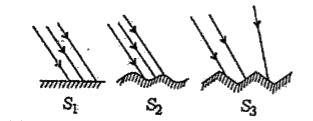
The surfaces on which the angle of incidence is equal to the angle of reflection areView SolutionThe number of ways of disturbing 10 different books among 4 students (S1−S4) such that S1andS2 gets 2 books and S3andS4 get 3 books each is:
View Solution

