Calculate magnitude of $Δ H$ in calorie for 1 mol of an ideal gas undergoing adiabatic reversible process from 8 atm, 300 K to 2 atm. (Given : $γ = 2, R = 2 C a l / K / m o l$ )

Text Solution

Verified by Experts

[0600]
$\frac{T_{2}}{T_{1}} = {(\frac{P_{1}}{P_{2}})}^{\frac{1 - γ}{γ}} = {(\frac{8}{2})}^{\frac{1 - 2}{2}} = {(\frac{4}{1})}^{\frac{- 1}{2}} = {(\frac{4}{1})}^{\frac{1}{2}} = \frac{1}{2}$
$T_{2} = 150 K$
$Δ H = 1 \times \frac{γ R}{γ - 1} (- 150) = \frac{2 \times 2}{1} \times (- 150) = - 600$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Calculate magnitude of work done in calorie for one mole of an ideal gas subjected to the process as shown in figure. [Use: $R = 2 c a l / m o l - K$ and ln $2 = 0.7$ ]

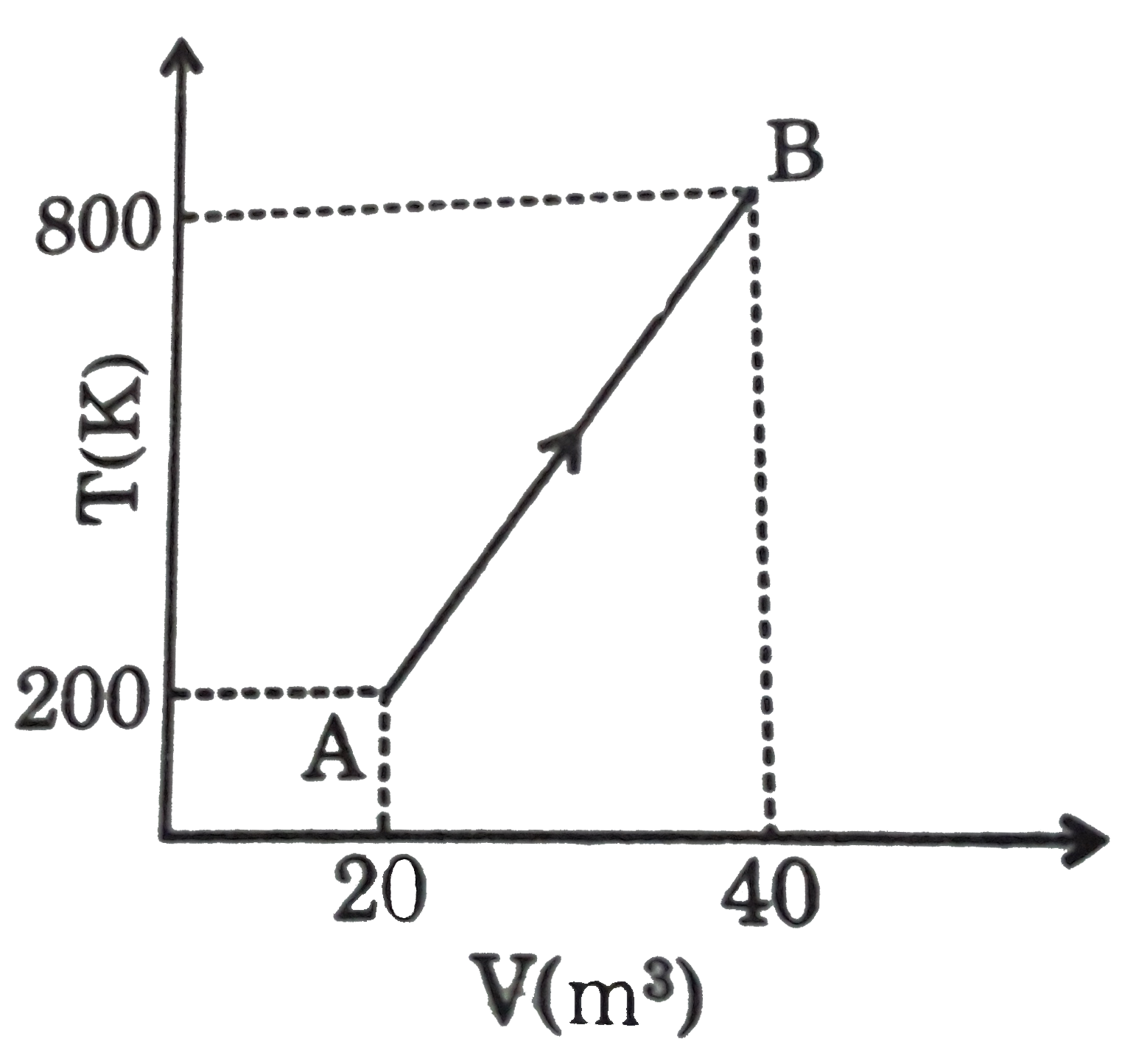A640 cal
B600 cal
C40 cal
D200 cal
Question 2 - Select One
1 mole of an ideal gas undergoes an isothermal reversible expansion form 10 atm to 1 atm at 300 K. What will be the work done ?
A $+ 57.44$ J
B $- 57.44$ J
C $- 5744$ J
D $+ 5744$ J
Question 3 - Select One
Calculate the final temperature of a monoatomic ideal gas that is compressed reversible and adiabatically from $16 L$ to $2 L$ at $300 K :$
A $600 K$
B $1044.6 K$
C $1200 K$
D $2400 K$

BANSAL-TEST PAPERS-CHEMISTRY SECTION-2 Part-C ( Integer type )

Home
Ask Doubt
Profile