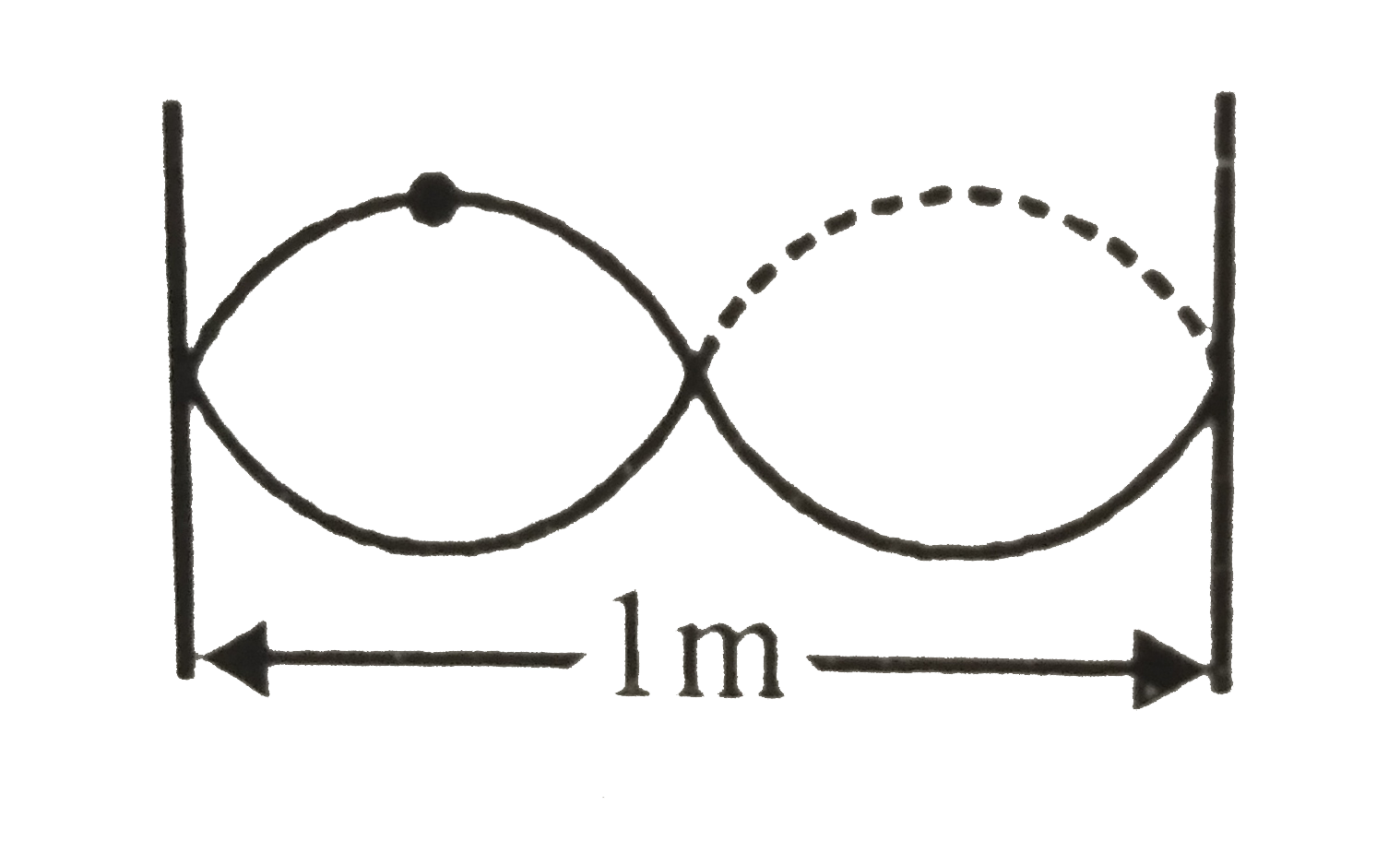
A steel wire is rigidly fixed at both ends its length mass and cross sectional area are 1m, 0.1 kg and $10^{6} m^{2}$ respectively then the temperature of the wire is lowered by $20^{\circ} C$ if the transverse waves are setup by plucking the wire at 0.25m from one end and assuming that wire vibrates with minimum number of loops possible for such a case. Find the frequency of vibration (in Hz). [coefficient of linear expansion of steel $= 1.21 \times 10^{- 6} / .^{\circ} C$ and young's modulus $= 2 \times 10^{11} / N / m^{2}$ ]

Video Solution

Text Solution

Verified by Experts

0022
$Δ L = L α Δ T$
for the condition minimum 2 loops will be formed
$∴ F = 2 f + (0), f = \frac{2}{2 L} \sqrt{\frac{Y A α Δ T}{\frac{M}{L}}} = \sqrt{\frac{Y A α Δ T}{M L}}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a stretched wire under tension and fixed at both ends, the area of cross section of the wire is halved and the tension is doubled. The frequency of the wire will be
Atwice
Bhalf
Cthree tiems
D3 times
Question 2 - Select One
A steel wire of length $1 m$ and mass $0.1 k g$ and having a uniform cross-sectional area of $10^{- 6} m^{2}$ is rigidly fixed at both ends. The temperature of the wire is lowered by $20^{\circ} C$ . If the wire is vibrating in fundamental mode, find the frequency (in Hz). $(Y_{s t e e l} = 2 \times 10^{11} N / m^{2}, α_{s t e e l} = 1.21 \times 10^{- 5} / .^{\circ} C)$ .
A11
B20
C15
D10
Question 3 - Select One
A sonometer wire of length $L$ is plucked at a distance $L / 8$ from one end then it vibrates with a minimum frequency $n$ . If the same wire plucked at a distance $L / 6$ from another end the minimum frequency with which it vibrates is
A $\frac{\sqrt{3}}{2} n$
B $\frac{3}{2} n$
C $\frac{3 n}{4}$
D $\frac{4 n}{3}$

BANSAL-TEST PAPERS-PHYSICS SECTION-1 Part-C (Integer Type )

Home
Ask Doubt
Profile