A cloud chamber is a device, which makes the tracks of moving charged particles visible. A light charged particle collides with a nucleus and rebounds elastically. Which of the momentum vector diagrams shown below indicates the event to a good approximation.
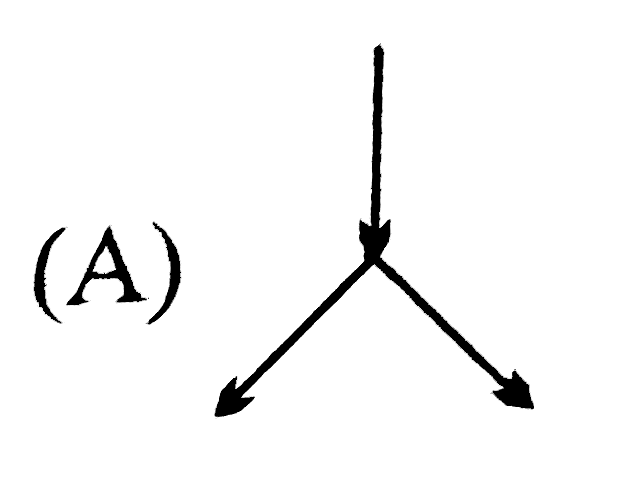
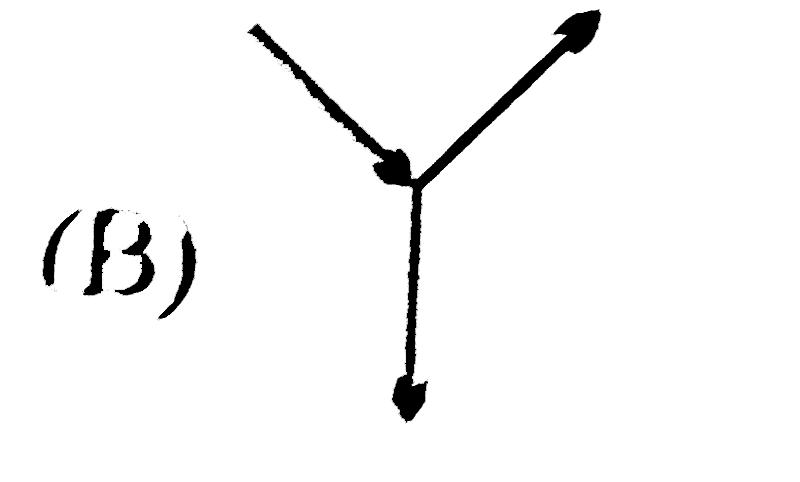
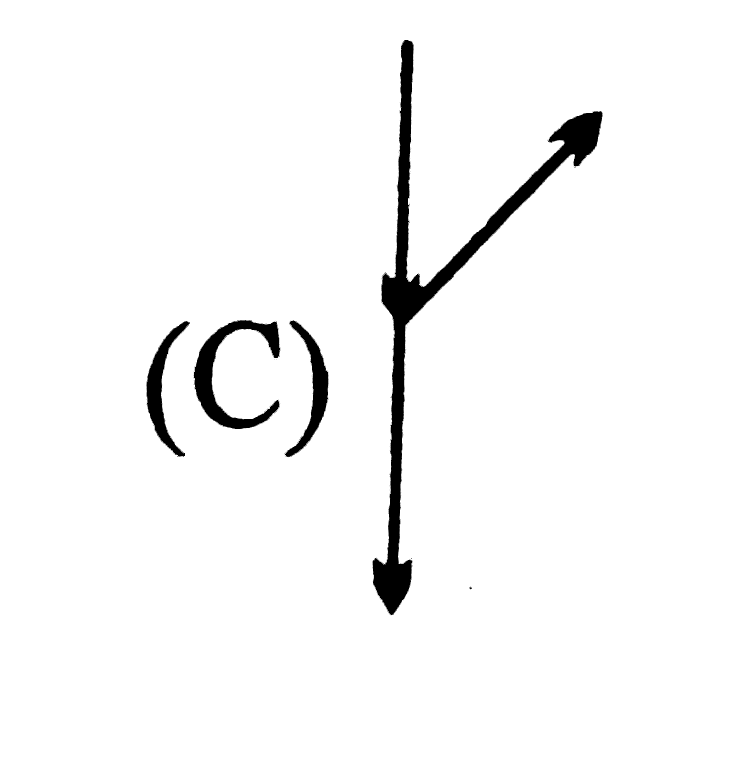
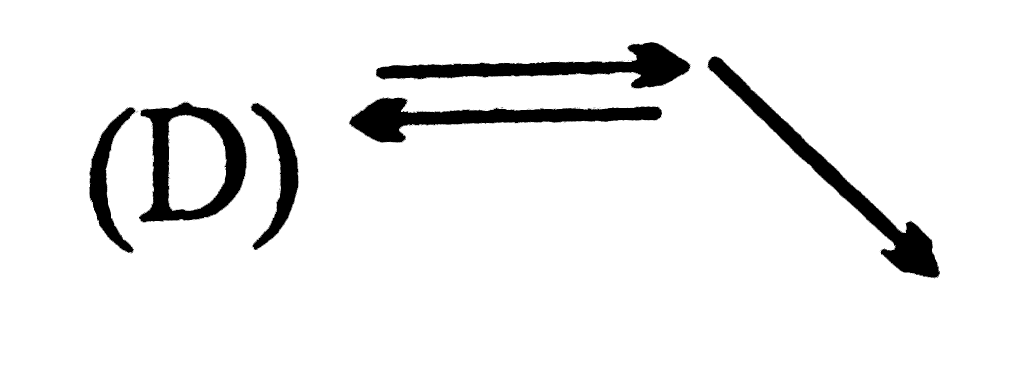
The correct Answer is:B
Momentum is conserved only in option A and B, A is ruled out, because charged particle is lighter than the nucleus (and not of same mass)
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY
133 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
58 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION - 2 [MULTIPLE CORRECT CHOICE TYPE]
6 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
Knowledge Check
A figure below shows the forces that three charged particles exert on each other. Which of the four situations shown can be correct .

 Aall of the aboveBnone of the aboveCII,IIIDII,III & IV
Aall of the aboveBnone of the aboveCII,IIIDII,III & IVA charge particle moves along the line AB, which lies in the same plane of a circular loop of conduting wire as shown in the fig . Then :
 ANo current will be induced in the loopBThe current inuced in the loop will change its direction as the charged particle passes byCThe current induced will be anticlockwiseDThe current induced , will be clockwise
ANo current will be induced in the loopBThe current inuced in the loop will change its direction as the charged particle passes byCThe current induced will be anticlockwiseDThe current induced , will be clockwiseA positively charged particle is moving with a speed v in the region of uniform magnetic induction field B as shown in figure. Which of the following statements is correct?
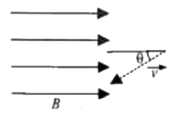 AThe force is Bqv sinθ perpendicular to B and in the plane of page.BThe force is Bqv cosθ perpendicular to the plane of the page and directed towards readerCThe force is Bqv sinθ perpendicular to the plane of the page and directed towards the reader.DThe force is Bqv sinθ perpendicular to the plane of the page and directed away from the reader
AThe force is Bqv sinθ perpendicular to B and in the plane of page.BThe force is Bqv cosθ perpendicular to the plane of the page and directed towards readerCThe force is Bqv sinθ perpendicular to the plane of the page and directed towards the reader.DThe force is Bqv sinθ perpendicular to the plane of the page and directed away from the reader
Rutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:

(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
An α-particle with initial speed v0 is projected from infinity and it approaches up to r0 distance from a nuclie. Then, the initial speed of α-particle, which approaches upto 2r0 distance from the nucleus is :
View SolutionRutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:

(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
An α-particle with initial speed v0 is projected from infinity and it approaches up to r0 distance from a nuclie. Then, the initial speed of α-particle, which approaches upto 2r0 distance from the nucleus is :
View SolutionRutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:

(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
Radius of a particular nucleus is calculated by the projection of α-particle from infinity at a particular speed. Let this radius is the true radius . If the radius calculation for the same nucleus is made by another α-particle with half of the earlier speed, then the percentage error involved in the radius calculation is :
View SolutionA particle with positive charge Q is held fixed at the origen. A second particle with positive charge q is fired at the first paricle, which follows the trajectory as shown in fig.

(a) Is the angular momentum of the second particular momentum of the second particle constant about some axis? Why or why not? Give reason to support your answer.
(b) Does the Coulomb force that one charge exerts on other charges changes if the other charges are brought nearby?(yes/No)
View SolutionA particle with positive charge Q is held fixed at the origen. A second particle with positive charge q is fired at the first paricle, which follows the trajectory as shown in fig.

(a) Is the angular momentum of the second particular momentum of the second particle constant about some axis? Why or why not? Give reason to support your answer.
(b) Does the Coulomb force that one charge exerts on other charges changes if the other charges are brought nearby?(yes/No)
View Solution
