Determine electric field intensity near an infinitely long straight uniformly charge wire.
Or.
Using Gauss' law expression for electric field intensity at a point situated at a distance 'r' from an infinitely long, uniformly charged straight wire.
Gauss law states that total eneric flux over the closed surface S in vacuum is 1ε0 times the total charge contained inside surface S.
ϕE=∮→E.−→dS=qε0
Electric field intensity due to a line charge.
COnsider a thin charged rod with uniform linear charge density λ. we wish to find an expression for electric intensity at point P at a perpendicular distance r, from the rod. consider a right circular cylinder of radius r and length l with the infinite long line of charge as its axis.
In surface I and III, →Eand−→dS are ⊥ to each other. in case of surface II, →Eand−→dS are parallel to each other and hence θ=0∘
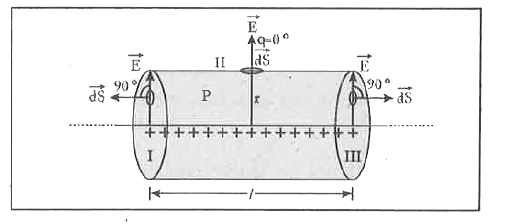
From Gauss.s theorem, we have
∮→E.−→dS=qε0
or ∮I→E.−→dS+∮II→E.−→dS+∮III→E.−→dS=qε0
or ∫IEdScos90∘+∫IIEdScos0∘+∫IIIEdScos90∘
=qε00
or 0+E∫IIdS+0=qε0
or E(2πrl)=qε0
or E=q2πr≤ψ0
But q=λl
∴E=λl2πr≤ψ0
or E=λ2πrε0
Topper's Solved these Questions
- ELECTROSTATICSBook:MBD -HARYANA BOARDChapter:ELECTROSTATICSExercise:OBJECTIVE TYPE QUESTIONS
Explore 23 Videos
- ELECTROSTATICSBook:MBD -HARYANA BOARDChapter:ELECTROSTATICSExercise:SHORT ANSWER TYPE QUESTIONS
Explore 11 Videos
- Electromagnetic WavesBook:MBD -HARYANA BOARDChapter:Electromagnetic WavesExercise:Example
Explore 7 Videos
- MAGNETISMBook:MBD -HARYANA BOARDChapter:MAGNETISMExercise:OBJECTIVE TYPE QUESTIONS
Explore 17 Videos
Similar Questions
Knowledge Check
Electric field 'E' at a point situated at a normal distacne 'r' from an infinitely long uniformaly charged straight were is proportional to
AE∞rBE∝1®CE∝1r2DE∝1r3Electric field of an infinitely long straight wire is proportional to:
ArB1r2C1r3D1rThe electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
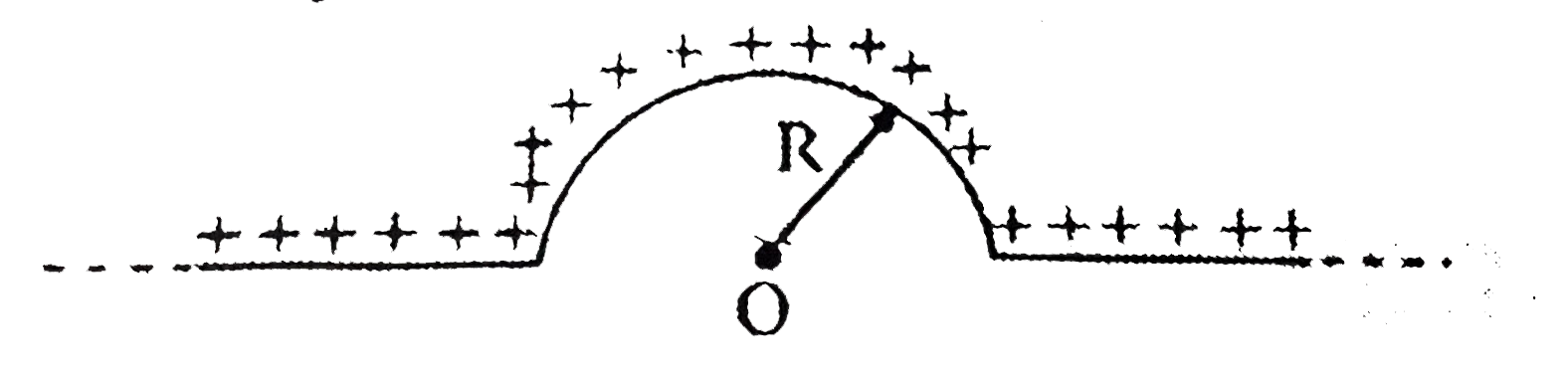 Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
Using Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View SolutionState Gauss's theorem in electrostatiics. State the expression for electric field intensity at a point outside an infinitely long charged conducting cylinder.
View SolutionUsing Gauss's law, derive an expression for the electric field intensity at any point near a uniformly charged thin wire of charge/length=λC/m.
View SolutionFind : (i)Electric field intensity due to an infinitely long uniformly charged, straight conductor , at a perpendicular distance d from rod.
(ii)Electric field intensity at a point on perpendicular bisector of uniformly charged rod of length l and charge Q at a distance d from the centre of rod.
View SolutionAnswer the following:
State Gauss' law in electrostatics. Derive an expression for the electric field due to an infinitely long straight uniformly charged wire.
View Solution
