State and prove Gauss's law in electrostatics.

Video Solution

Text Solution

Verified by Experts

Gauss.s Theorem. It states that the total electric flux through any closed surface is equal to $\frac{1}{ε_{0}}$ times the total electric charge enclosed by the surface.
Mathematically,
$ϕ = \oint \to E . d \to S = \frac{q}{ε_{0}}$
Proof. Consider a closed spherical surface S and a point charge +q be placed at its centre O as shown in the figure. consider a small element of area dS around point P through which the electric flux $d ϕ$ is given by
$d ϕ = \to E, d \to S$

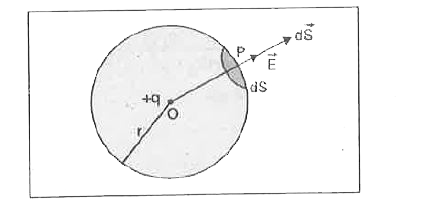
Total electric flux linked whole closed surface S will be
$ϕ = \oint d ϕ = \oint \to E . d \to S$
or $ϕ = \oint E d S {cos 0}^{\circ} = \oint E d S$ . . (i)
The electric field intensity E at P due to charge q at O is given by
$E = \frac{1}{4 π ε_{0}} \frac{q}{r^{2}}$ . . (ii)
Putting Eq. (ii) in Eq. (i), we get
$ϕ = \oint \frac{1}{4 π ε_{0}} \frac{q}{r^{2}} d S$
$= \frac{1}{4 π ε_{0} r^{2}} \oint d S$
$= \frac{1}{4 π ε_{0} r^{2}} 4 π r^{2}$
or $ϕ = \frac{q}{ε_{0}}$
This is Gauss theorem.
Coulomb.s law from Gauss Theorem
Consider an isolated positive charge +q at O. imagine a sphere of radius r and centre O.
Electric field $\to E$ at every point on the sphere is the same and is directed outwards. direction of small area element $- \to d S$ is also along $\to E$ i.e., the angle between $\to E$
and $- \to d S$ is $0^{\circ}$ ,
According to Gauss theorem,
$\oint_{S} \to E . - \to d S = \frac{q}{ε_{0}}$

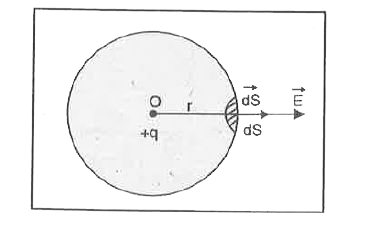
or $\oint_{S} E d S {cos 0}^{\circ} = \frac{q}{ε_{0}}$
or $E \oint_{S} d S = \frac{q}{ε_{0}}$
or $E \times 4 π r^{2} = \frac{q}{ε_{0}}$
or, $E = \frac{q}{4 π ε_{0} r^{2}}$
If another charge $q_{0}$ is placed on the sphere then force F on it is
$F = q_{0} E = \frac{q_{0} q}{4 π ε_{0} r^{2}}$
which is coulomb.s law.

Updated on:21/07/2023

What is the nature of Gaussian surface involved in Gauss's law of electrostatics?
AScalar
BElectrical
CMagnetic
DVector
The unity of the electriec and magnetic waves was found by Maxwell from
(i) Guss's law in electrostatics
(ii) Gauss's law in magnetism
(iii) Faraday's law of electromagnetic induction.
(iv) Ampere's law with displacement current.
A(i) and (iii) only
B(iii) and (iv) only
Call
DVelocity of light also