If the radius of an octahedral void is r and the radius of atom is close packing is R, derive the relationship between r and R.

Text Solution

Verified by Experts

The radius of the sphere representing an octahedral void can be calculated by considering the cross-section through void. The cross-section of the octahedron is a square and it is shown in Fig.
Let the radius of octahedral void is r and the radius of sphere is R. In the isosceles triangle ABC,
$\frac{A C}{A B} = \frac{\sqrt{2}}{1}$

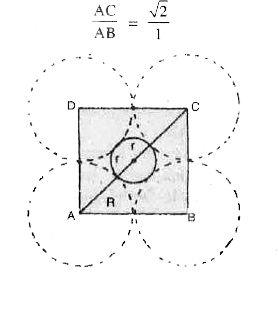
Now, AB = 2R
AC = R + 2r +R
$∴ \frac{2 R + 2 r}{2 R} = \frac{\sqrt{2}}{1}$
or $1 + \frac{r}{R} = \frac{\sqrt{2}}{1}$
or $\frac{r}{R} = \sqrt{2} - 1 = 0.414$
or r= 0.414 R
Thus, for an atom to occupy an octahedral void, its radius must be 0.414 times the radius of the sphere.

Updated on:21/07/2023