If the radius of the octahedral void is r and radius of the atoms in close-packing is R, derive relation between r and R.
The relation between r and R for octahedral void is derived as under :
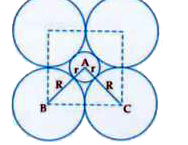
A sphere fitting into an octahedral void is shown in the Fig. For clarity, the spheres above and below have been removed. ABC is a right angled triangle.
∴ BC2=AB2+AC2
or (2R)2=(R+r)2+(R+r)2=2(R+r)2
or (2R)22=(R+r)2
or (2√2R)2=(R+r)2
or R+r=√2R
or r=√2R−R
or r=R(√2−1)
or r=0.414R
Topper's Solved these Questions
- SOLID STATEBOOK - U-LIKE SERIESCHAPTER - SOLID STATEEXERCISE - CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS
14 Videos
- SOLID STATEBOOK - U-LIKE SERIESCHAPTER - SOLID STATEEXERCISE - MULTIPLE CHOICE QUESTIONS
20 Videos
- SOLID STATEBOOK - U-LIKE SERIESCHAPTER - SOLID STATEEXERCISE - SELF ASSESSMENT TEST
8 Videos
- SAMPLE QUESTIONS PAPER BOOK - U-LIKE SERIESCHAPTER - SAMPLE QUESTIONS PAPER EXERCISE - SECTION D
6 Videos
- SOLUTIONBOOK - U-LIKE SERIESCHAPTER - SOLUTIONEXERCISE - SELF ASSESSMENT TEST (SECTION D)
2 Videos
Similar Questions
Knowledge Check
If the radius of the octaheral void is r and the radius of the atoms in close-packing is R, derive relation between r and R
Ar=0.414RBR=0.414rCr=2RDr=√2RIf the radius of the octahedral void is r and radius of the atom in closet packed structure is R then
Ar/R=0.414Br/R=0.225Cr/R=0.155Dr/R=0.732
If the radius of the octaheral void is r and the radius of the atoms in close-packing is R, derive relation between r and R
View SolutionIf the radius of a tetrahedral void is 'r' and radius of atom in close packing is 'R', derive the relation between r and R.
View Solution(a) If the radius of octahedral void is r and the radius of the atoms in the close packing is R, derive a relationship between r and R.
(b) What is a semiconductor? Describe the two main types of semiconductors and conductor and contrast conduction mechanism in them.
View SolutionIf the radius of an octahedral void is r and the radius of atom is close packing is R, derive the relationship between r and R.
View Solution(a) If the radius of octahedral void is 'r' and the radius of the atoms in close packing is 'R' what is the relation between 'r' and 'R' ?
(b) A metal crystallises in body centred cubic structure. If 'a' is the edge length of its unit cell, 'r' is the radius of the sphere, what is the relation between 'r' and 'a' ?
View Solution(a) If the radius of octahedral void is 'r' and the radius of the atoms in close packing is 'R' what is the relation between 'r' and 'R' ?
(b) A metal crystallises in body centred cubic structure. If 'a' is the edge length of its unit cell, 'r' is the radius of the sphere, what is the relation between 'r' and 'a' ?
View Solution
