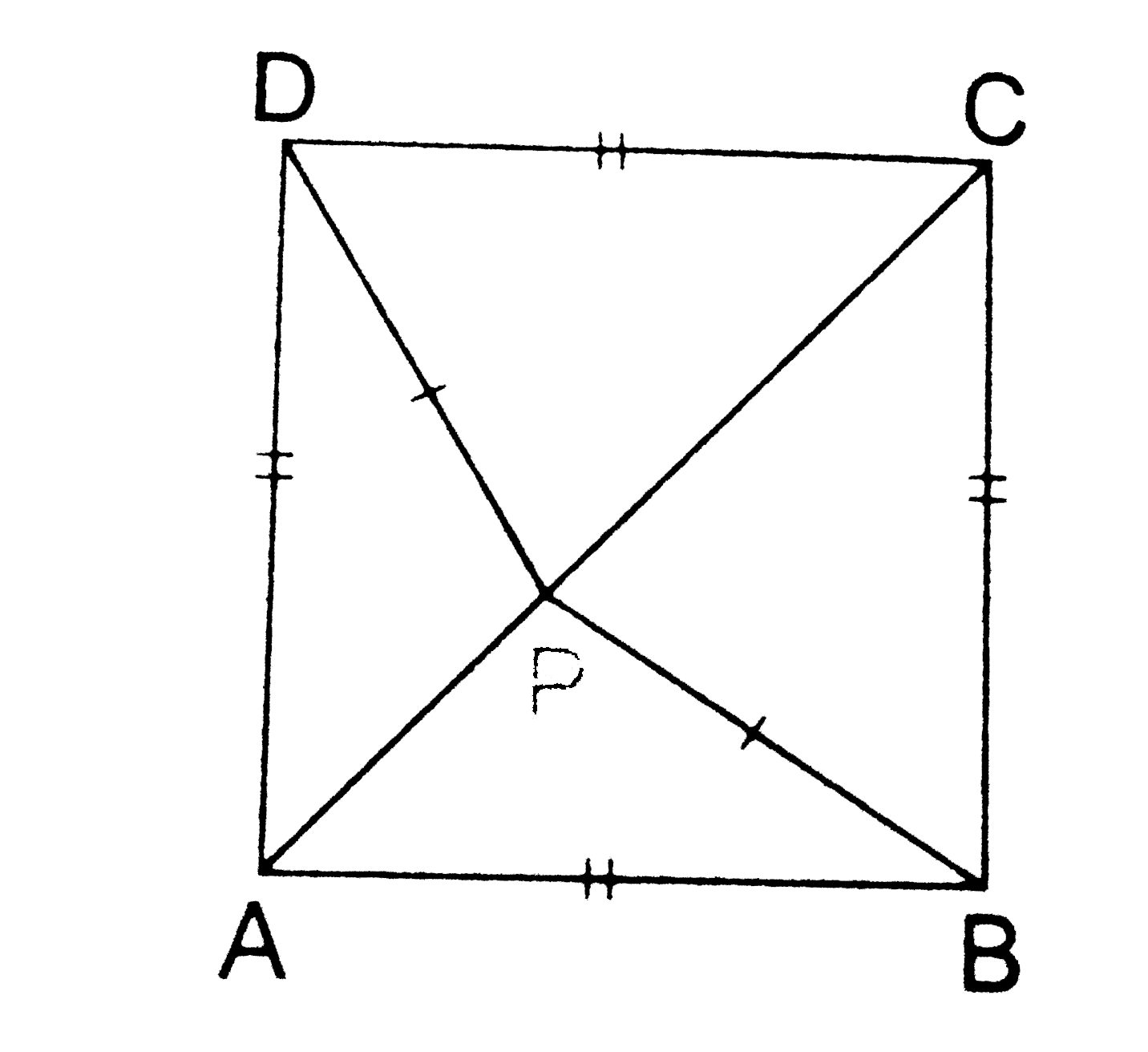
P is an interior point of square ABCD. Prove that PA+PB+PC+PD>2AB.
Step by step video & image solution for P is an interior point of square ABCD. Prove that PA+PB+PC+PD gt 2 AB. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level-1
Explore 24 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level-2
Explore 26 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Short answer Type Question
Explore 29 Videos
- FORMULASBook:PEARSON IIT JEE FOUNDATIONChapter:FORMULASExercise:ASSESSMENT TESTS (Test 2)
Explore 8 Videos
- INDICES Book:PEARSON IIT JEE FOUNDATIONChapter:INDICES Exercise:Test -2
Explore 12 Videos
Similar Questions
Knowledge Check
If P is a point inside a convex quadrilateral ABCD such that PA2+PB2+PC2+PD2 is twice the area of the quadrilateral , then the correct statements is/ are
APA, PB , PC all are equalBABCD must be a square and P must be its centreCABCD must be a square but P may be its centreDABCD may not be squareLet ABCD be a square and let P be point on segment CD such that DP : PC = 1 : 2. Let Q be a point on segment AP such that ∠BQP=90∘. Then the ratio of the area of quadrilateral PQBC to the area of the square ABCD is
A3160B3760C3960D4160
[" An equilateral triangle "ABC" is inscribed in a circle.P is any point on the minor are BC.Prove "],[" that "PA=PB+PC]
View SolutionIn the given figure, ABCD is a square and P is a point inside it such PB = Pd. Prove that CPA is a straight line.
View SolutionIn the given Fig. 5, from an external point P, a tangent PT and a secant PAB is drawn to a circle with centre 0. ON is perpendicular on the chord AB. Prove that PA.PB=PT2?.

View SolutionThere is a point P in a rectangle ABCD, such that PA = 4, PD = 5, PB = 8, find PC.
View SolutionIf P be a point in the interior of equilateral triangle ABC such that PA=3, PB=4andPC=5 then find a.
View SolutionIn the given figure, ABCD is a parallelogram. Point P is at BC such that PB : PC = 1 : 2. The extended DP and extended AB meets at point Q. If the area of BPQ is 20 unit2 then find the area of ΔDCP.
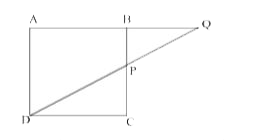
View Solution