There is a point P in a rectangle ABCD, such that PA = 4, PD = 5, PB = 8, find PC.
The correct Answer is:√73
To solve the problem of finding the length PC in rectangle ABCD with point P inside it, we can use the following steps:
1. Identify the Given Values:
- PA=4
- PD=5
- PB=8
- We need to find PC.
2. Use the Formula:
In a rectangle, the relationship between the distances from a point inside the rectangle to the vertices is given by the formula:
PA2+PC2=PD2+PB2
3. Substitute the Known Values:
Substitute the known values into the formula:
42+PC2=52+82
4. Calculate the Squares:
- Calculate 42:
42=16
- Calculate 52:
52=25
- Calculate 82:
82=64
5. Set Up the Equation:
Substitute the calculated squares back into the equation:
16+PC2=25+64
6. Simplify the Right Side:
Combine the numbers on the right side:
25+64=89
So, the equation becomes:
16+PC2=89
7. Isolate PC2:
Subtract 16 from both sides to isolate PC2:
PC2=89−16
PC2=73
8. Take the Square Root:
To find PC, take the square root of both sides:
PC=√73
Final Answer:
Thus, the length PC is √73 cm.
---
- PA=4
- PD=5
- PB=8
- We need to find PC.
In a rectangle, the relationship between the distances from a point inside the rectangle to the vertices is given by the formula:
PA2+PC2=PD2+PB2
Substitute the known values into the formula:
42+PC2=52+82
- Calculate 42:
42=16
- Calculate 52:
52=25
- Calculate 82:
82=64
Substitute the calculated squares back into the equation:
16+PC2=25+64
Combine the numbers on the right side:
25+64=89
So, the equation becomes:
16+PC2=89
Subtract 16 from both sides to isolate PC2:
PC2=89−16
PC2=73
To find PC, take the square root of both sides:
PC=√73
Thus, the length PC is √73 cm.
Topper's Solved these Questions
- QUADRILATERALBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - QUADRILATERALEXERCISE - EXERCISE
48 Videos
- PROFIT & LOSSBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PROFIT & LOSSEXERCISE - Questions
200 Videos
- RATIO & PROPORTIONBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - RATIO & PROPORTIONEXERCISE - QUESTIONS
113 Videos
Similar Questions
Knowledge Check
If P is a point within a rectangle ABCD, then:
AAP2+PC2=BP2+PD2BAP2+BP2=PC2+PD2CAP+PC=BP+PDDAP×PC=BP×PDIf P is a point within a rectangle ABCD, then:
AAP2+PC2=BP2+PD2BAP2+BP2=PC2+PD2CAP+PC=BP+PDDAP×PC=BP×PDO is the centre of a circle. There is a point P in the region of the circle. If PA = PB = PC where A, B and C are points on the circumference of the circle, then OP must be equal to :
APA+PB+PC3BPA+PB+PC2CAB+BC2Dzero
ABC is an equilateral triangle where AB = a and P is any point in its plane such that PA = PB + PC. Then PA2+PB2+PC2a2 is
View SolutionIf P is a point on the plane of ΔABC such that ¯¯¯¯¯¯PA+¯¯¯¯¯¯PB+¯¯¯¯¯¯PC=0, then, for Δ ABC, the point P is
View SolutionPA and PB are two tangents drawn from point P to circle of radius 5 . A line is drawn from point P which cuts at C and D such that PC=5 and PD=15 and ∠APB=θ.
On the basis of above information answer the questions .
Area of ΔAPB is
View SolutionIf P is a point in th e plane of D ABCD such that ¯¯¯¯¯¯AP+¯¯¯¯¯¯PB+¯¯¯¯¯¯CP+¯¯¯¯¯¯PD=¯0, then the quadrilateral is in general, a
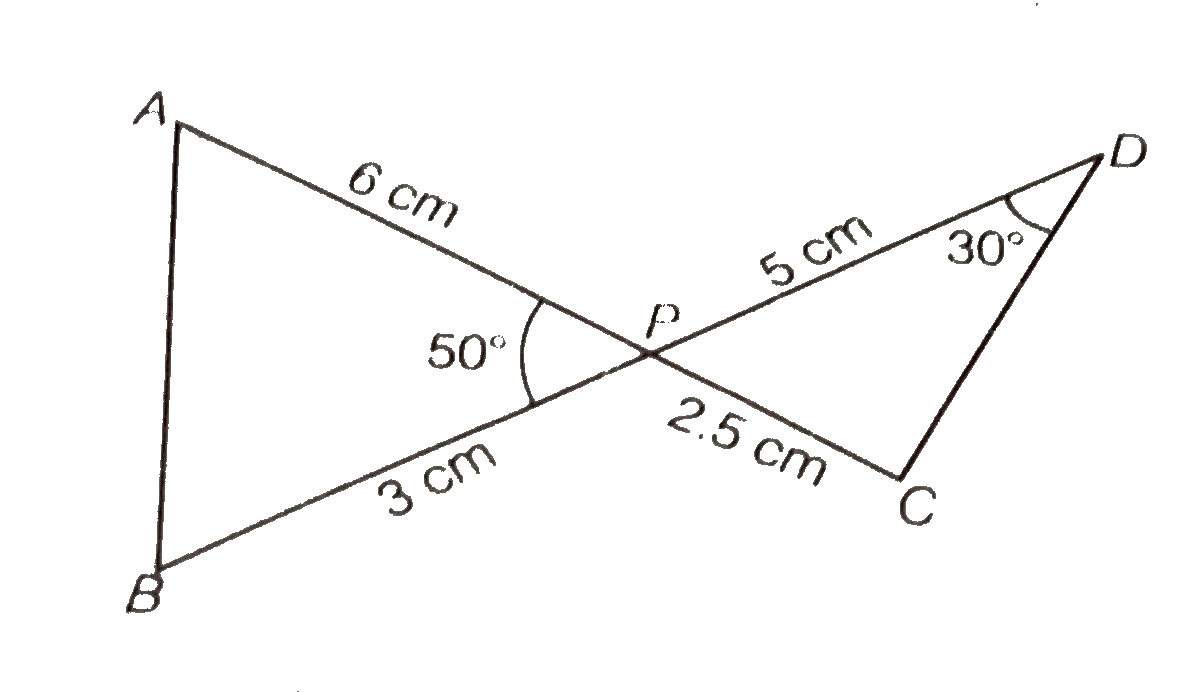
View SolutionIn figure, two line segments AC and BD intersects each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD=5 cm, ∠APB=50∘ and ∠CDP=30∘. Then, ∠PBA is equal to
View Solution
