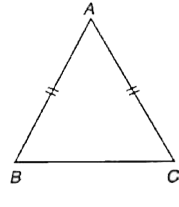
In an isosceles triangle ABC, AB=AC and ∠A=3∠B. Find ∠C.
36∘
32∘
28∘
40∘
The correct Answer is:A
Given AB=AC
⇒∠B=∠C
Also given ∠A=3∠B
We have, ∠A+∠B+∠C=180∘
3∠B+∠B+∠B=180∘
⇒∠B=36∘
∴∠C=36∘
Hence, the correct option is (a).
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-319videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-112videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-124videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)8videos
FORMULAS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -212videos
INDICES
Similar Questions
Knowledge Check
- Question 1 - Select One
In an isosceles triangle ABC,∠B=90∘ and side AB=6cm. Side AC will be
A6 cmB12 cmC2√6 cmD6√2 cm
Triangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
AO is bisector of ∠AView SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
OB=OCView SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
OB=OCView SolutionIn an isosceles ΔABC if ∠A=90∘ and AB=AC, find ∠B and ∠C.
View SolutionIn Figure, ABC is an isosceles triangle with AB=AC and m ∠ABC=500. Find m ∠BDC and ∠BEC
View SolutionIn a triangle ABC, ∠A<∠B,∠B>∠C and ∠A=2∠C, prove that AC>BC>AB.
View SolutionIn the figure, ABC is an isosceles triangle in which AB = AC and LM is parallel to BC. If ∠A=50∘ find ∠LMC.
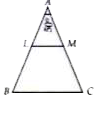 View Solution
View Solution