In a quadrilateral ABCD, and AB=AD. ABCD is a ________
A
trapezium
B
rhombus
C
rectangle
D
Kite
Video Solution
Text Solution
The correct Answer is:D
The given quadrilateral is a kite.
Hence, the correct option is (d).
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-212videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-319videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)8videos
FORMULAS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -212videos
INDICES
Similar Questions
Knowledge Check
- Question 1 - Select One
M and N are mid-point of the diagnols AC and BD respectivley of quadrilateral ABCD, then¯¯¯¯¯¯AB+¯¯¯¯¯¯AD+¯¯¯¯¯¯CB+¯¯¯¯¯¯CD=
A2¯¯¯¯¯¯¯¯MNB2¯¯¯¯¯¯¯¯NMC4¯¯¯¯¯¯¯¯MND4¯¯¯¯¯¯¯¯NM - Question 2 - Select One
In a quadrilateral ABCD, AC is the bisector of the (AB, AD) which is 2π3, 15|AC|=3|AB|=5|AD|, then cos(BA,CD) is equal to
A−√147√2B−√217√3C2√7D2√714
In the figure 11.34, ABCD is a quadrilateral in which ¯¯¯¯¯¯AB=¯¯¯¯¯¯ADand¯¯¯¯¯¯BC=¯¯¯¯¯¯DC. Diagonals ¯¯¯¯¯¯ACandBD intersect each other at O.Show that-
View SolutionIn a quadrilateral ABCD, AB= AD and CB = CD, prove that AC is perpendicular bisector of BD.
View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View Solution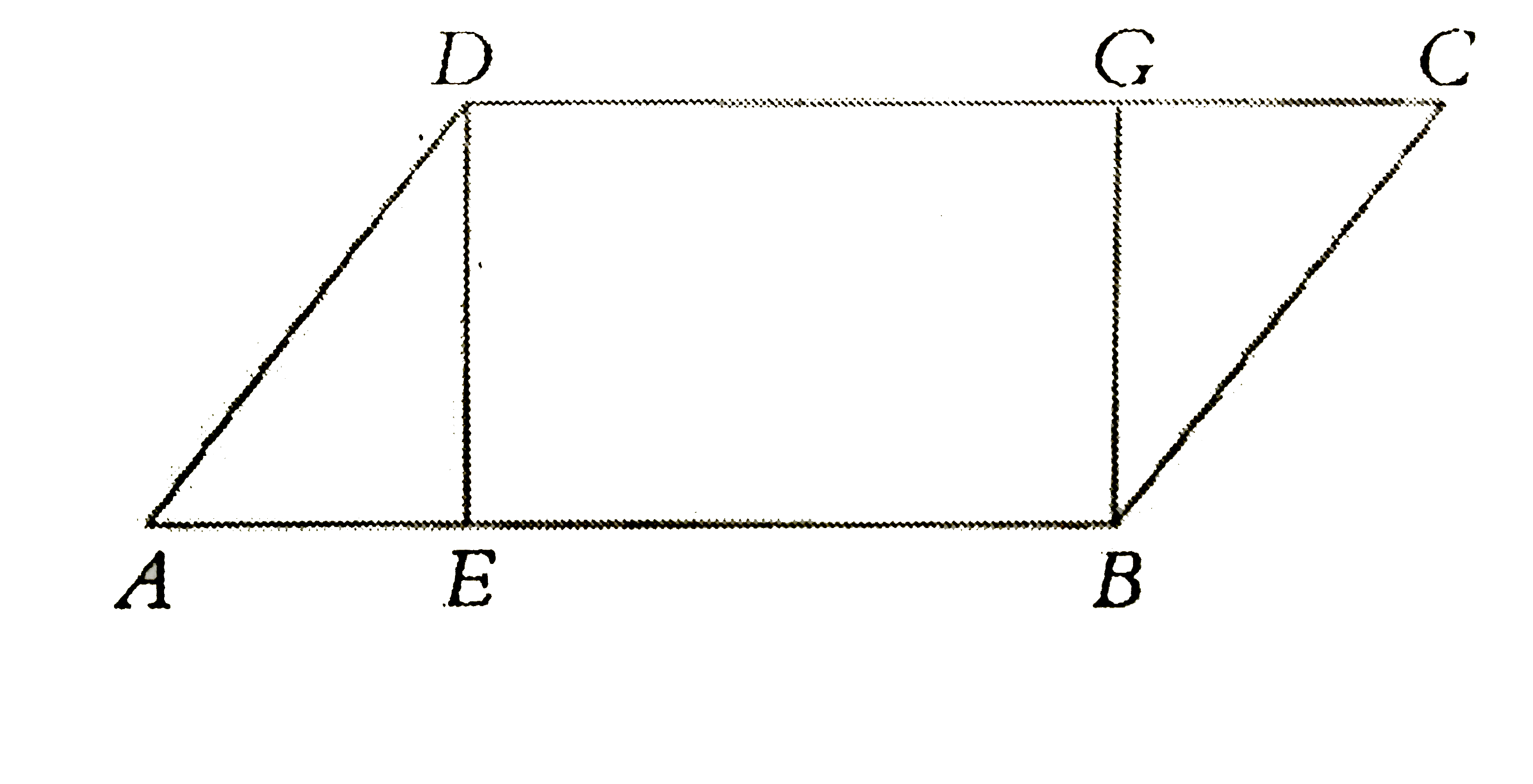
In the figure above, ABCD is a parallelogram, ¯¯¯¯¯¯BE⊥¯¯¯¯¯¯AB,¯¯¯¯¯¯BG⊥¯¯¯¯¯¯CD, and EBGD is a square. If BG=12 cm and BC=13 cm , then find AB.View SolutionShow that in a quadrilateral ABCD ,AB+BC+CD+DA<2(BD+AC)
View Solution

