In a quadrilateral ABCD, show that
(AB+BC+CD+DA)>(AC+BD).

Joint AC. Then,
AB+BC>ACandCD+DA>AC.
∴ (AB+BC+CD+DA)>2AC. …(i)
Similarly, by joining BD, we get
(AB+BC+CD+DA)>2BD ...(ii)
Adding respective sides of (i) and (ii), we get the required result.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A27videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)37videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)22videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
In a cyclic quadrilateral ABCD, AB = BC, AD = DC, AC⊥BD,∠CAD=θ. Then ∠ABC will be-
AθBθ2C2θD3θ
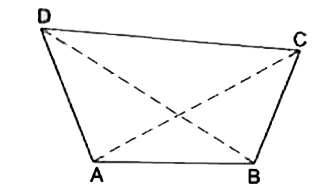
The given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD
 View Solution
View SolutionABCD is a quadri,aterial prove that (AB+BC+CD+DA)>(AC+BD)
 View Solution
View SolutionShow that in a quandrilateral ABCD,AB+BC+CD+DA<2(BD+AC).
View SolutionIn quadrilatcal ABCD, prove that AB+BC+CD+AD<2(BD+AC)
View SolutionIn a quadrilateral ABCD prove that AB2+BC2+CD2+DA2=AC2+BD2+4PQ2 where P and Q are middle points of diagonals AC and BD.
View SolutionThe given figure shows a quadrilateral ABCD such that AB = CD = 4 cm. The length of AC is 6 cm.
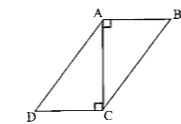
What is the area of the quadrilateral ABCD?View SolutionIn a quadrilateral ABCD, it is given that AB∣∣CD and the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View Solution

