Find a unit vector perpendicular to each of the vector $\to a + \to b$ and $\to a - \to b$ , where $\to a = 3 ˆ i + 2 ˆ j + 2 ˆ k$ and $\to b = ˆ i + 2 ˆ j - 2 ˆ k$ .Solution in Tamil

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\pm (\frac{2}{3} ˆ i - \frac{2}{3} ˆ j - \frac{1}{3} ˆ k)$

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Find a unit vector perpendicular to each of the vector vec a+ vec b and vec a - vec b, where vec a = 3 hat i + 2 hat j + 2 hat k and vec b = hati + 2 hat j - 2 hat k. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.1
2 Videos
VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.2
13 Videos
VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.3
18 Videos
TRIGONOMETRIC FUNCTIONSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - QUESTIONS FROM COMPETITIVE EXAMS
134 Videos

Similar Questions

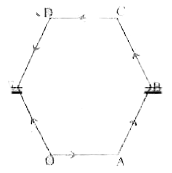
In the figure which vectors are
(i) equal (ii) collinear (iii) coinitial

View Solution
Compute the magnitude of the following vectors and identify the unit vector.
$\to a = 2 ˆ i - 3 ˆ j + 5 ˆ k$
View Solution
Find the angle between two vectors $\to a$ and $\to b$ with magnitudes $\sqrt{3}$ and 2, respectivey having $\to a . \to b = \sqrt{6}$ .
View Solution
If $A + B + C = 90^{\circ}$ then
$\frac{cot A + cot B + cot C}{cot A cot B cot C}$ =
View Solution
Let $\to a = ˆ j - ˆ k$ and $\to c = ˆ i - ˆ j - ˆ k$ . Then vector $\to b$ satisfying $\to a \times \to b + \to c = \to 0$ and $\to a . \to b = 3$ is (1) $2 \to i - \to j + 2 \to k$ (2) $ˆ i - ˆ j - 2 ˆ k$ (3) $ˆ i + j - 2 ˆ k$ (4) $- ˆ i + ˆ j - 2 ˆ k$
View Solution
Find a unit vector perpendicular to both of the vectors $\to a + \to b$ and $\to a - \to b$ where $\to a = ˆ i + ˆ j + ˆ k, \to b = ˆ i + 2 ˆ j + 3 ˆ k .$
View Solution
If $\to a = ˆ i + 2 ˆ j + 3 ˆ k$ and $\to b = 2 ˆ i + 3 ˆ j + ˆ k$ , find a unit vector in the direction of $(2 \to a + \to b)$ .
View Solution
Find the unit vectors perpendicular to both $\to a$ and $\to b$ when
(i) $\to a = 3 ˆ i + ˆ j - 2 ˆ k$ and $\to b = 2 ˆ i + 3 ˆ j - ˆ k$
(ii) $\to a = ˆ i - 2 ˆ j + 3 ˆ k$ and $\to b = ˆ i + 2 ˆ j - ˆ k$
(iii) $\to a = ˆ i + 3 ˆ j - 2 ˆ k$ and $\to b = - ˆ i + 3 ˆ k$
(iv) $\to a = 4 ˆ i + 2 ˆ j - ˆ k$ and $\to b = ˆ i + 4 ˆ j - ˆ k$
View Solution
Find the projection of vector $(\to b + \to a)$ on vector $\to a$ where $\to a = 2 ˆ i - ˆ j + 2 ˆ k and \to b = ˆ j + 2 ˆ k$
View Solution
सदिश $(\to a + \to b)$ और $(\to a - \to b)$ में से प्रत्येक के मात्रक सदिश ज्ञात कीजिए जहाँ $\to a = ˆ i + ˆ j + ˆ k, \to b = ˆ i + 2 ˆ j + 3 ˆ k$ है।
View Solution
Given $\to a = 4 ˆ i - ˆ j + 3 ˆ k$ and $\to b = - 2 ˆ i + ˆ j - 2 ˆ k$ .
(i) Find a unit vector perpendicular to both $\to a$ and $\to b$ .
(ii) Find a vector of magnitude 9 which is perpendicular to both $\to a$ and $\to b$ .
View Solution
For given vectors $\to a = 2 ˆ i - ˆ j + 2 ˆ k$ and $\to b = - ˆ i + ˆ j - ˆ k$ , find the unit vector in the direction of the vector $\to a + \to b$ .
View Solution
If $\to a = ˆ i + ˆ j + ˆ k$ , $\to b = 2 ˆ i - ˆ j + 3 ˆ k$ and $\to c = ˆ i - 2 ˆ j + ˆ k$ , find a unit vector parallel to the vector $2 \to a - \to b + 3 \to c$
View Solution
For given vector, $\to a$ = 2 $ˆ i$ $j$ +2 $ˆ k$ and $\to b$ = - $ˆ i$ + $ˆ j$ - $ˆ k$ , find the unit vector in the direction of the vector $\to a$ + $\to b$ .
View Solution
If $\to a = ˆ i + ˆ j + ˆ k, \to b = 2 ˆ i - ˆ j + 3 ˆ k a n d \to c = ˆ i - 2 ˆ j + ˆ k$ find a unit vector parallel to $2 \to a - \to b + 3 \to c$
View Solution
Let $\to a = ˆ j - ˆ k$ and $\to c = ˆ i - ˆ j - ˆ k$ . Then vector $\to b$ satisfying $\to a \times \to b + \to c = \to 0$ and $\to a . \to b = 3$ is (1) $2 \to i - \to j + 2 \to k$ (2) $ˆ i - ˆ j - 2 ˆ k$ (3) $ˆ i + j - 2 ˆ k$ (4) $- ˆ i + ˆ j - 2 ˆ k$
View Solution

NEW JOYTHI PUBLICATION-VECTOR ALGEBRA-SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.4

Find |vec a xx vec b| if vec a = hat i -7 hat j + 7 hat k and vec b = ...
02:08
Find a unit vector perpendicular to each of the vector vec a+ vec b a...
04:49
If a unit vector vec a makes angles(pi)/(3) with hat i , (pi)/(4) with...
14:53
Show that (vec a - vec b) xx (vec a + vec b) = 2 (vec a xx vec b)
01:20
Find lambda amd mu if (2 hat i + 6 hat j+ 27 hat k) xx (hat i + lambda...
01:48
Given that vec a. vec b = 0 and vec a xx vec b = vec 0. What can you c...
01:36
Let the vectors veca, vecb, vec c be given as a(1)hat i + a(2)hatj + a...
15:02
If either vec a = vec 0 or vec a xx vec b = vec 0 .Is the converse tr...
05:02
Find the area of the triangle with vertices A(1,1,2)B(2,3,5) and C(1,5...
01:52
Find the area of the parallelogram whose adjacent sides are determined...
02:38
Let the vectorsvec a and vec b be such that |veca| = 3 and |vecb| = (s...
01:58
Area of a rectangle having vertices A,B,C and D with positions vectors...
08:02

Home
Ask Doubt
Profile

Find a unit vector perpendicular to each of the vector →a+→b and →a−→b, where →a=3ˆi+2ˆj+2ˆk and →b=ˆi+2ˆj−2ˆk.Solution in Tamil

The correct Answer is:±(23ˆi−23ˆj−13ˆk)

Topper's Solved these Questions

Similar Questions

NEW JOYTHI PUBLICATION-VECTOR ALGEBRA-SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.4

Find a unit vector perpendicular to each of the vector $\to a + \to b$ and $\to a - \to b$ , where $\to a = 3 ˆ i + 2 ˆ j + 2 ˆ k$ and $\to b = ˆ i + 2 ˆ j - 2 ˆ k$ .Solution in Tamil

The correct Answer is: $\pm (\frac{2}{3} ˆ i - \frac{2}{3} ˆ j - \frac{1}{3} ˆ k)$