Find λ amd μ if (2ˆi+6ˆj+27ˆk)×(ˆi+λj+μk)=→0.Solution in Tamil
The correct Answer is:Hence λ=3,μ=272
Step by step video, text & image solution for Find lambda amd mu if (2 hat i + 6 hat j+ 27 hat k) xx (hat i + lambda j + mu k) = vec 0. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.1
2 Videos
- VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.2
13 Videos
- VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.3
18 Videos
- TRIGONOMETRIC FUNCTIONSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - QUESTIONS FROM COMPETITIVE EXAMS
134 Videos
Similar Questions
In the figure which vectors are
(i) equal (ii) collinear (iii) coinitial
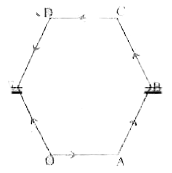
View SolutionCompute the magnitude of the following vectors and identify the unit vector.
→a=2ˆi−3ˆj+5ˆk
View SolutionFind the angle between two vectors →a and →b with magnitudes √3 and 2, respectivey having →a.→b=√6.
View SolutionIf A+B+C=90∘ then
cotA+cotB+cotCcotAcotBcotC =
View SolutionDetermine whether the following pair of lines intersect or not. (1) →r=ˆi−5ˆj+λ(2ˆi+ˆk);→r=2ˆi−ˆj+μ(ˆi+ˆj−ˆk) (2) →r=ˆi+ˆj−ˆk+λ(3ˆi−ˆj);→r=4ˆi−ˆk+μ(2ˆi+3ˆk)
View SolutionIf →a=2ˆi+6ˆj+3ˆk,→b=ˆi+λˆj+μˆk. If →a×→b=0 , find the value of λ and μ.
View SolutionFind the shortest distance between the given line
→r=(ˆi+ˆj)+λ(2ˆi−ˆj+ˆk)
→r=(2ˆi+ˆj−ˆk)+μ(3ˆi−5ˆj+2ˆk)
View SolutionFind the shortest distance between the given line
→r=(λ−1)ˆi+(λ+1)ˆj+(λ+1)ˆk
vec(r ) =(1−μ)ˆi+(2μ−1)ˆj+(μ+2)ˆk.
View Solutionयदि (2ˆi+6ˆj+27ˆk)×(ˆi+λˆj+μˆk)=0 तो λ तथा के μ के मान ज्ञात कीजिए।
View SolutionIf the vectors →a=2ˆi−λˆj+3ˆk,→b=3ˆi+2ˆk−μˆk and →c=ˆi+ˆj+ˆk are coplanar , find μ in terms of λ
View SolutionFind 'λ' and 'μ' if :
(ˆi+3ˆj+9ˆk)×(3ˆi−λˆj+μˆk)=ˆ0.
View SolutionFind λ and μif (2ˆi+6ˆj+27ˆk)×(ˆi+λˆj+μˆk)=→0.
View SolutionFind the shortest distance between the lines →r=(ˆi+2ˆj+ˆk)+λ(ˆi−ˆj+ˆk) and →r=(2ˆi−ˆj−ˆk)+μ(2ˆi+ˆj+2ˆk)
View SolutionDetermine whether the following pair of lines intersect or not. (1) →r=ˆi−5ˆj+λ(2ˆi+ˆk);→r=2ˆi−ˆj+μ(ˆi+ˆj−ˆk) (2) →r=ˆi+ˆj−ˆk+λ(3ˆi−ˆj);→r=4ˆi−ˆk+μ(2ˆi+3ˆk)
View SolutionFind λ and μ if (2ˆi+6ˆj+27ˆk)×(ˆi+λˆj+μˆk)=ˆ0.
View Solution
