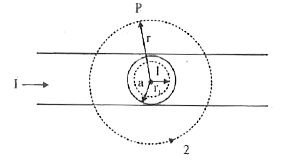
Figure shows a long straight wire of a circular cross - section (radius a) carrying steady current I. The current I is uniformly distributed across this cross - section . Calculate the magnetic field in the region r<a and r>a
 Solution in Tamil
Solution in Tamil
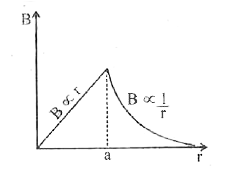
I When r<a (i.e inside ), B=(μ0i2πa2)r
[For part I shown in fig, the current enclosed , i.e , =i×πr2πa2. Applying Ampere.s theorem, B.2πr=μ0ir2a2∴B=(μ0i2πa2)r] when r>a , B×2πr=μ0i∴B=μ0i2πr
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NEW JOYTHI PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CONTINUOUS EVALUATION
1 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NEW JOYTHI PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CONTINUOUS EVALUATION (ASSIGNMENT)
4 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NEW JOYTHI PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - PRACTICE PROBLEMS FOR SELF ASSESSMENT
20 Videos
- MAGNETISM AND MATTERBOOK - NEW JOYTHI PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - COMPETITIVE EXAM CORNER
13 Videos
- NUCLEIBOOK - NEW JOYTHI PUBLICATIONCHAPTER - NUCLEIEXERCISE - COMPETITIVE EXAM CORNER
23 Videos
Similar Questions
Construction of a voltmeter to read required voltage and an ammeter to read required current, by converting a Galvanometer
View SolutionOutline the Oersted's experiment.
View SolutionA vertical wire carries a current of 17 A. If the neutral point is observed at a distance of 10 cm from the wire, calculate the horizontal compoinent of earth's magnetic field .
View SolutionChoose the correct statement .
View SolutionRadioactive 6027Co is transformed into stable 6028Ni by emitting two γ - rays of energies
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionFigure shows the circular cross-section of a long straight wire of radius a carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r lt a (dashed inner circle) and r gt a (dashed outer circle).
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of a circular cross - section (radius a) carrying steady current I. The current I is uniformly distributed across this cross - section . Calculate the magnetic field in the region r lt a and r gt a
View SolutionThe adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for (i) r lt a , (ii) r gt a .
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r a.
View SolutionA long straight wire of a circular cross-section (radius r) carries a steady current I. The current is distributed uniformly across the cross-section. Calculare the magnetic field at a point (a) outside the wire , (b) inside the wire. Draw a graph showing variation of magnetic field.
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionA long straight wire of a curcular cross-section of radius 'a' carries a steady current 'l'. The current is uniformly distributed the across- section . Apply Amphere's circuital law to calculate the magnetic field at a point 'r' in the region for (i) r lt a and (ii) r gt a .
View SolutionA long straight wire of radius 'a' carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetic fields at a/2 and 2a is
View Solution
