Question

A particle of mass (m) is moving with constant velocity (v). Show that its angular momentum about any point renains constant throughout the motion.

Explanation

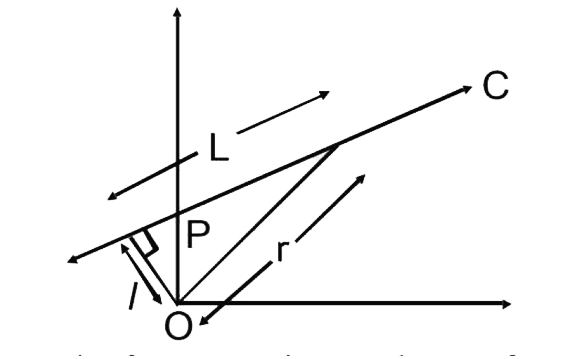
Let the particle of mass m move with constant velocity 7. As it is moving with constant velocity, its path is a straight line. Its momentum `(vecP = m vecv)` is also directed along the same path. Let us fix an origin (O) at a perpendicular distance (d) from the path. At a particular instant, we can connect the particle which is at position with a position Vector `vecr= bar(OQ)`.
Take, the angle between the `vec r and vec q` as `theta`. The magnitude of angular momentum of that particle at that instant is,
`L= OQ p sin theta= QO mv sin theta =mv (OQ sin theta)`

The term `(OQ sin theta)` is the perpendicular distance (d) between the origin and line along which the mass is moving. Hence, the angular momentum of the particle about the origin is,
`L = mvd`
The above expression for angular momentum L. does not have the angle. As the momentum ( p m ) and the perpendicular distance (d) are constants, the angular momentum of the particle is also constant. Hence, the angular momentum is associated with bodies with linear notion also. If the straight path of the particle passes through the origin, then the angular momentum is zero, which is also a constant.