A piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg Solution in Tamil
Step by step video & image solution for A piece of wood of mass m is floating erect in a liquid whose density is rho . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2pisqrt((m)/(Arhog)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONS BOOK - FULL MARKSCHAPTER - OSCILLATIONS EXERCISE - ADDITIONAL QUESTIONS SOLVED
51 Videos
- OSCILLATIONS BOOK - FULL MARKSCHAPTER - OSCILLATIONS EXERCISE - ADDITIONAL QUESTIONS SOLVED (2-MARKS QUESTIONS )
8 Videos
- OSCILLATIONS BOOK - FULL MARKSCHAPTER - OSCILLATIONS EXERCISE - TEXTUAL EVALUATION SOLVED ( III LONG ANSWER QUESTIONS )
10 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENT BOOK - FULL MARKSCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENT EXERCISE - ADDITIONAL QUESTIONS SOLVED ( SHORT ANSWER QUESTIONS (2 MARK))
20 Videos
- PROPERTIES OF MATTERBOOK - FULL MARKSCHAPTER - PROPERTIES OF MATTEREXERCISE - Additional Questions Solved - Numerical Questions
19 Videos
Similar Questions
The total energy of a particle vibrating in SHM is proportional to the square of its………..
View SolutionWhat is Oscillatory motion?
View SolutionWhat is meant by simple harmonic oscillation ? Give example
View SolutionThe vernier scale of a travelling microscope has 50 divisions which coincide with 49 main scale divisions. If each main scale division is 0.5 mm. Calculate the minimum inaccuracy in the measurement of distance.
View SolutionTwo steel wires of lengths 1 m and 2 m have diameters 1 mm and 2mm respectively . If they are stretched by force of 40 N and 80 N respectively, find the ratio of their elongations.
View SolutionA plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
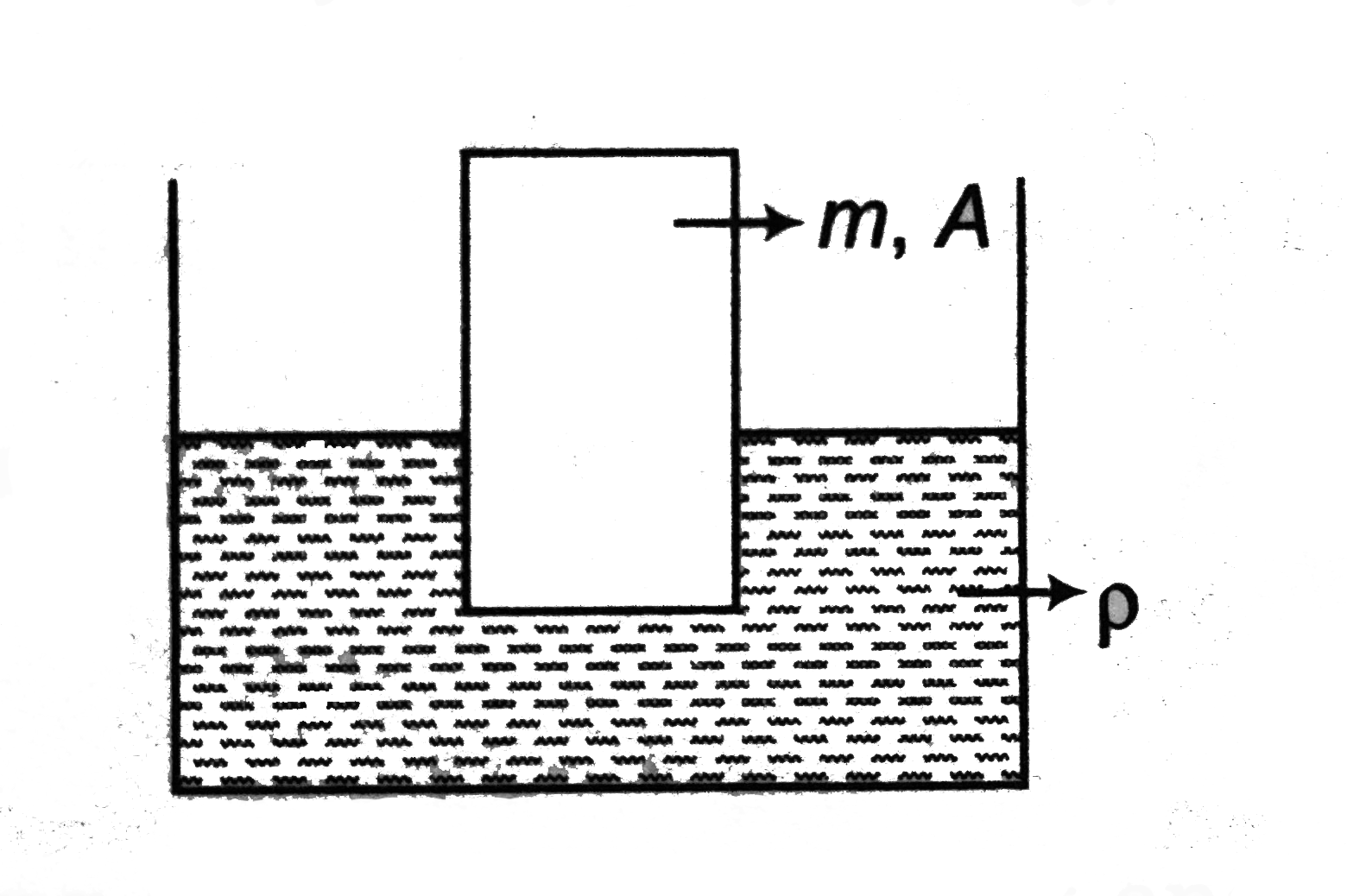
View SolutionA cylinderical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a tiem period. T=2pisqrt((m)/(Arhog) where m is mass of the body and rho is density of the liquid.
View SolutionA cylidrical wooden piece of cork floats in a liquid of density σ. The cork is depressed slightly and released. Show that the cork will oscillate up and down simple harmonicaly with a period.
T=2π√ρhσg, where ρ is the density of the cork.
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA cylindrical piece of cork of density rho , base area A and height h, floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically, with a period T=2pisqrt((hrho)/(rho_(1)g)) , where 'rho' is the density of the cork.
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA piece of wood of mass m is floating erect in a liquid whose density is ρ . If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T=2π√mAρg
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density p1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density pl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. The cork oscillates up and down simple harmonically with period is (ρ is the density of cork)
View Solution
