Derive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.Solution in Tamil
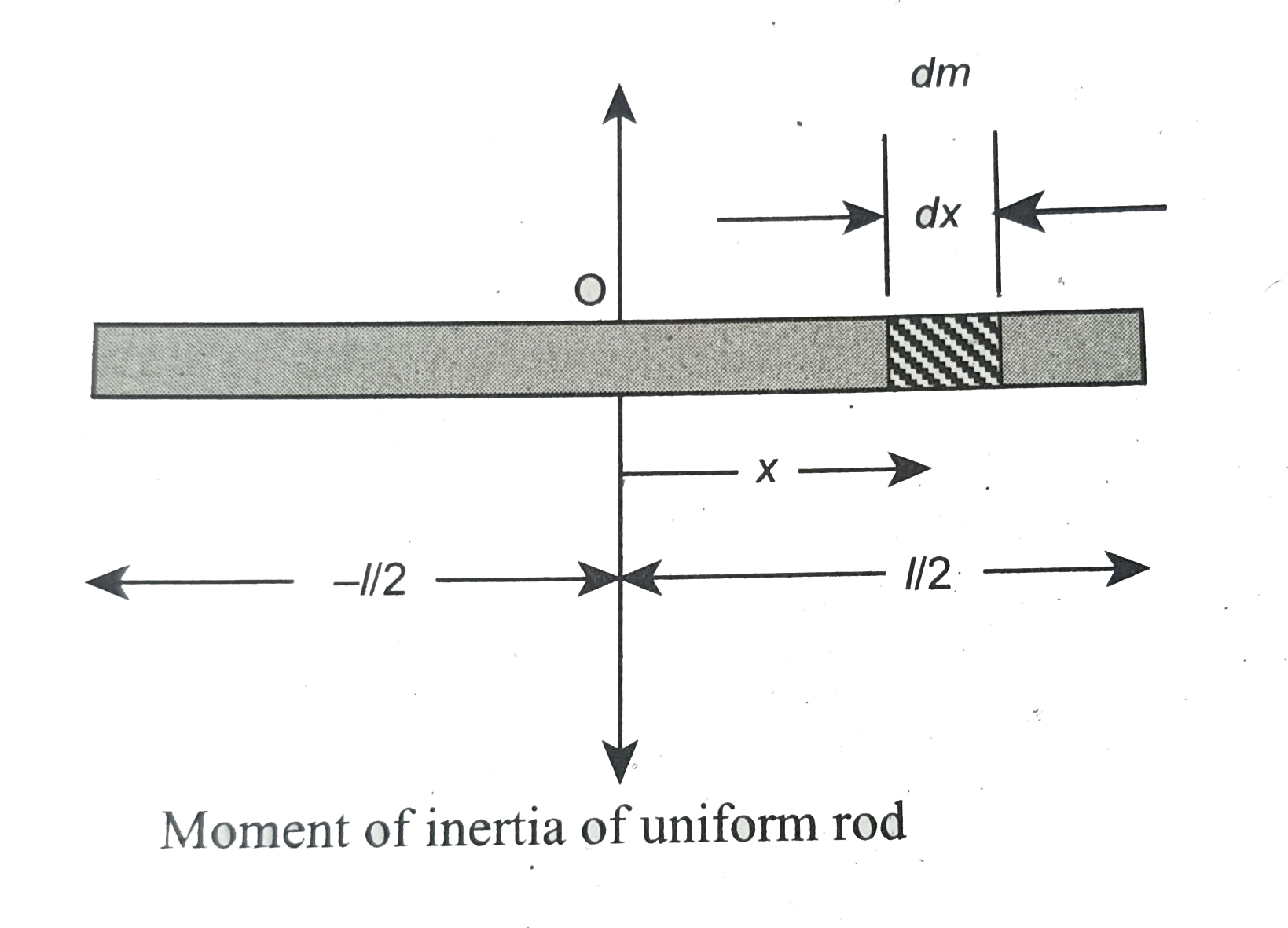
Let us consider a uniform rod of mass (M) and length (l) as shown in figure. Let us find an expression for moment of inertia of this rod about an axis that passes through the center of mass and perpendicular to the rod. First an origin is to be fixed for the coordinate system so that it coincides with the center of mass, which is also the geometric center of the rod. The rod is now along ther axis. We take an infinitesimally small mass (dm) at a distance (x) fromn the origin. The moment of inertia (dl) of this mass (dm) about the axis is,
dI=(dm)x2
As the mass is uniformly distributed, the mass per unit length (λ) of the rod is, λ=Ml
The (dm) mass of the infinitesimally small length as d(m)=λdx=Mldx
The moment of inertia (i) of the entire rod can be found by integrating dl,
I=∫(dI)=∫(dm)x2=∫(Mldx2)x2
I=Ml∫x2dx
As the mass is distributed on either side of the origin, the limits for integration are taken from to l/2 to l/2.
∫l/2−l/2x2dx=Ml[x33]l/2−l/2
I=Ml[(l324−(−(l324)]=Ml[(l324+(l324)]<br>I= (M)/(l) 2[(l^(3)/(24)] , I= (1)/(12)Ml^(2)
Topper's Solved these Questions
Similar Questions
What are the limitations of dimensional analysis?
View SolutionThe force F acting on a body moving in a circular path depends on mass of the body (m) velocity(v) and radius (r) of the circular path. Obtain the expression for the force by dimensional analysis method (k=1)
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionState the expression for the moment of inertia of a thin uniform disc about an axis perpendicular to its plane and through its centre. Hence deduce the expression for its moment of inertia about a tangential axis perpendicular to its plane.
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionDerive the expression for moment of inertia of a uniform ring about an axis passing thorugh the centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionDerive the expression for moment of inertia of a uniform ring about an axis passing thorugh the centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inertia of a uniform ring about an axis passing thorugh the centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.
View Solution
