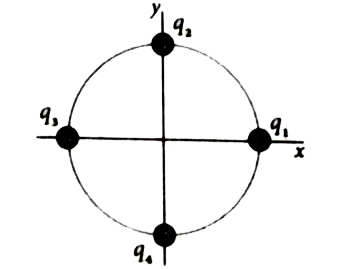
Consider four equal charges q1,q2,q3 and q4=q=+1μC located at four different points on a circle of radius 1m , as shown in the figure. Calculate the total force acting on the charge q1 due to all the other charges .
 Solution in Tamil
Solution in Tamil
According to the superposition principle the total electrostatic force on charge q1 is the vector sum of the forces due to the other charges,
→Ftot1=→F12+→F13+→F14
The following diagram shows the direction of each force on the charge q1
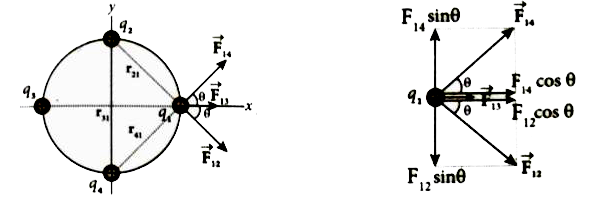
The charges q2 and q4 are equi-distant from q1 . As a result the strengths ( magnitude ) of the forces →F12 and →F14 are the same even though their directions are different . Therefore the vectors representing these two forece are drawn with equal length . But the charge q3 is located farther compared to q2 and q4 . Since the strength of the electrostatic force decreases as distance increases the strength of the force →F13 is drawn with smaller length compared to that for forces →F12 and →F14 .
From the figure r21=√2m=r41and r31=2m
The m agnitudes of the forces are given by
F13=kq2r331=9×109×10−124=2.25×10−3N
F12=kq2r221=F14=9×109×10−122=4.5×10−3N
From the figure the angle θ=45∘ . In terms of the components we have
→F12=F12cosθˆi−F12sinθˆj=4.5×10−3×1√2ˆi−4.5×10−3×1√2ˆj
→F13=F13ˆi=2.25×10−3Nˆi
→F14=F14cosθˆi+F14sinθˆj=4.5×103×1√2ˆi+4.5×10−3×1√2ˆj
Then the total force on q1 is
→Ftot1=(F12cosθˆi−F12sinθˆj)+F13ˆi+(F14cosθˆi+F14sinθˆj)
→Ftot1=(F12cosθ+F13+F14cosθ)ˆi+(−F12sinθ+F14sinθ)ˆj
Since F12=F14 the jth component is zero . Hence we have
→Ftot1=(F12cosθ+F13+F14cosθ)ˆi
Substituting the values in teh above equation
=4.5√2+2.25+4.5√2ˆi=(4.5√2+2.25)ˆi
→Ftot1=8.61×10−3Nˆi
The resultant force is along the positive x axis .
Topper's Solved these Questions
- BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - Textual Evaluation Solved (Multiple choice questions : )15videos
ELECTROSTATICS
- BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - Textual Evaluation Solved (II. Short Answer Questions : )21videos
ELECTROSTATICS
- BOOK - FULL MARKSCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ADDITIONAL QUESTIONS -( ADDITIONAL NUMERICAL PROBLEMS : )10videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - ADDITIONAL QUESTIONS SOLVED - NUMERICAL PROBLEMS :4videos
MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT
Similar Questions
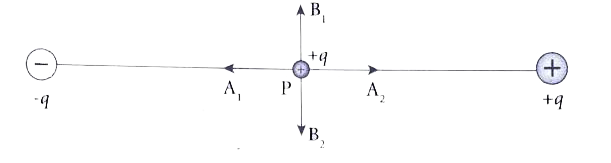
Two identical point charges'of magnitude -q are fixed as shown in the figure below. A third charge +q is placed midway between the two charges at the point P. Suppose this charge is displaced a small distance from the point P in the directions indicated by the arrows, in which direction(s) will +q be stable with respect to the displacement?
 04:48View Solution
04:48View SolutionWhat is meant by quantisation of charges ?
02:03View SolutionIf a light of wavelength 4950 Å is viewed as a continuous flow of photons, what is the energy of each photon in eV ? (Given h=6.6×10−34Js, c =3×108ms−1)
03:14View SolutionThe radius of the first orbit of hydrogen atom is 0.5 Å. The electron moves is an orbit with a uniform speed of 2.2×106ms−1. What is the magnetic field produced at the centre of the uncleus due to the mation of this electron ? Use μ0=4π×10−7Hm−1 and electric charge =1.6×10−19 C
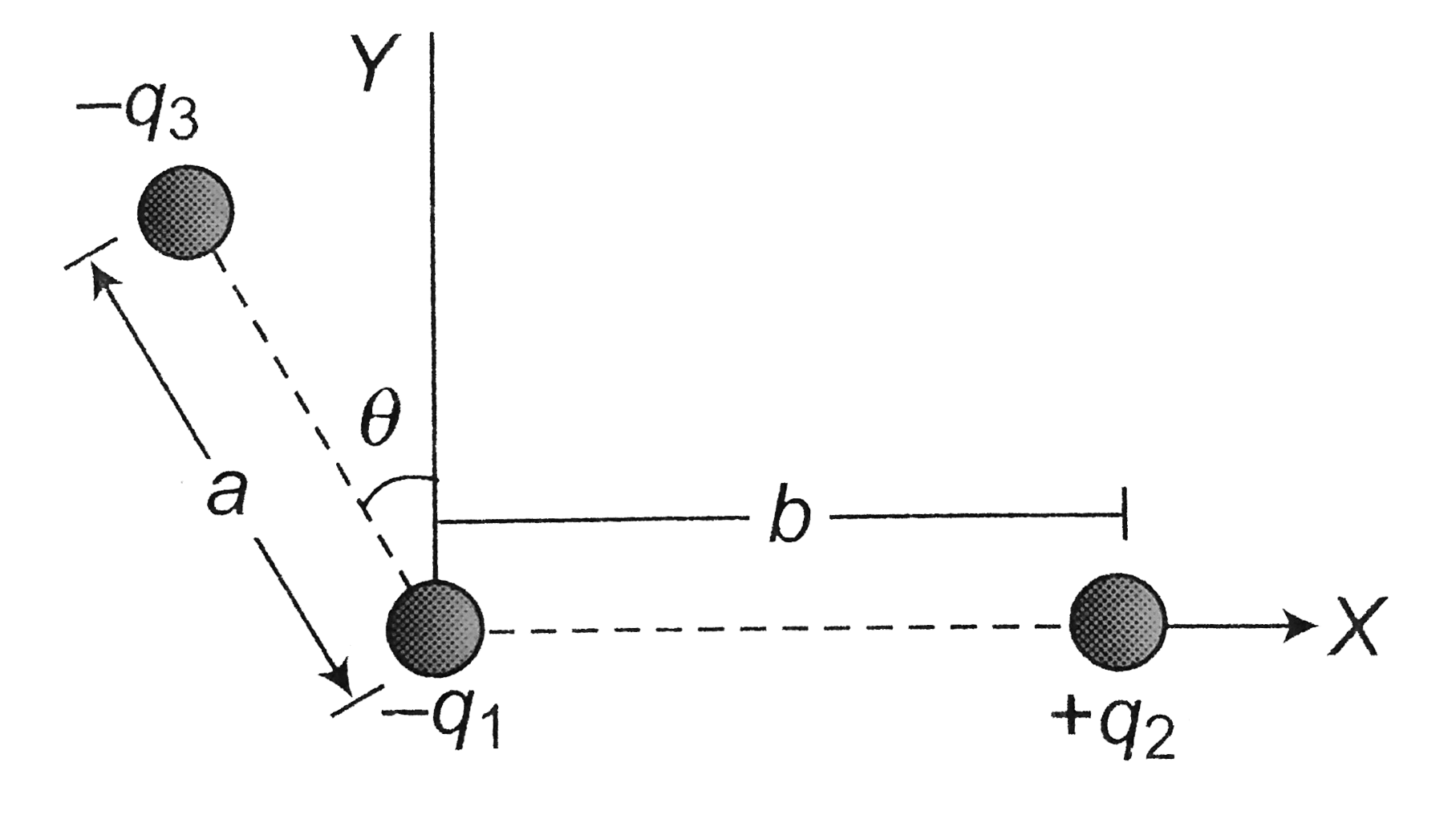
10:46View SolutionThree charges -q_(1), +q_(2) and -q_(3) are placed as shown in the figure. The x -component of the force on -q_(1) is proportional to
02:12View SolutionTwo large , parallel conducting plates X and Y , kept close to each other , are given Q1 and Q2(Q1>Q2). The four surfaces of the plates are A,B,C and D , as shown

(i) The charge on A is 12(Q1+Q2)
(ii) The charge on B is 12(Q1−Q2)
(iii) The charge on C is 12(Q2−Q1)
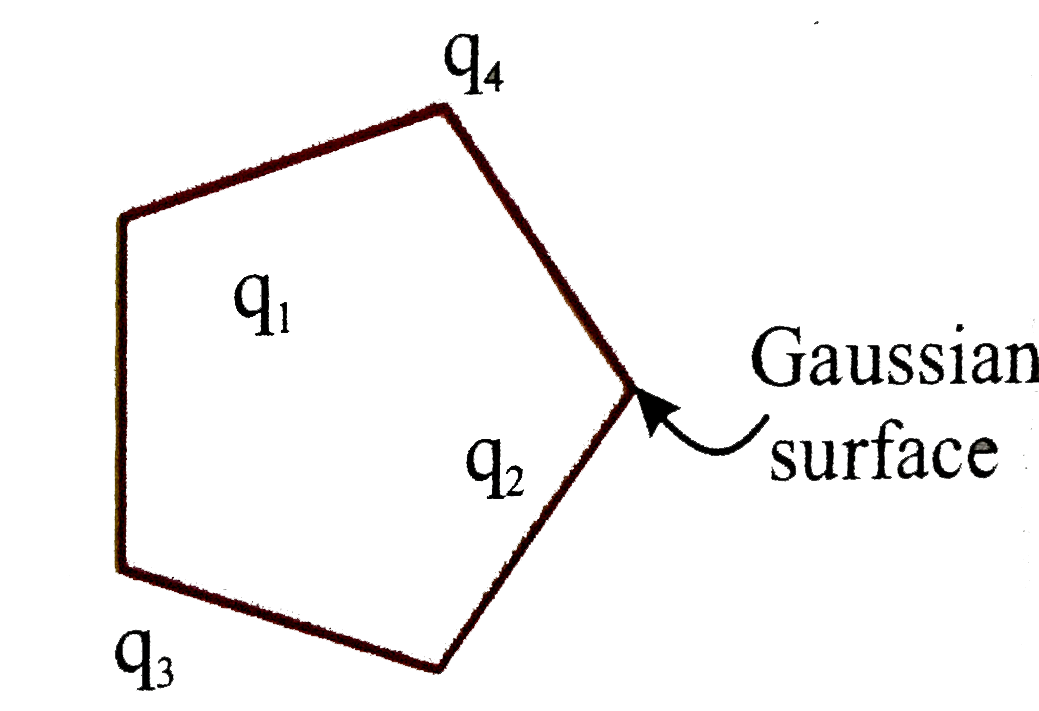
(iv) The charge on D is 12(Q1+Q2)05:11View SolutionAssertion: Four point charges q1,q2,q3 and q4 are as shown in Fig,The flux over the shown Gaussians surface depends only on charges q1 and q2
Reason:Electric field at all points on Gaussians surface depends on any charges q1 and q2
 04:48View Solution
04:48View SolutionThree charges q_(1) = 1 mu C, q_(2) = -2 muC and q_(3) = 3mu C are placed on the vertices of an equilateral triangle of side 1.0 m. find the net electric force acting on charge q_(1) . How to proceed Charge q_(2) will attract charge q_(1) (along the line joining them) and charge q_(3) will repel charge q_(1) . Therefore, two forces will act on q_(1) , one due to q_(2) and another due to q_(3) . Since , the force is a vector quantity both of these force (say F_(1) and F_(2) ) will be added by vector method. Following are two methods of their addition
04:01View SolutionA charge q1 exerts some force on a second charge q2 If a third charge q3 is brought near q2, then the force exterted by q1 on q2
02:59View SolutionRepresent the resultant force acting on a charge q0 due to point charges q1,q2,q3,q4. Assume the position vectors as →r0,→r1,→r2,→r3,→r4 respectively. Give the expression for net force on q0
04:58View SolutionThree charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
 04:05View Solution
04:05View Solutionचित्र 2.52 में सभी चार आवेशों का परिमाण एक जैसा है। बिन्दु P पर इन द्वारा उत्पन्न वैद्युत क्षेत्र बाईं दिशा में हैं। आवेश q1 ऋणात्मक है। आवेशों q2,q3 और q4, के क्या चिह्न हैं?
 03:07View Solution
03:07View Solutionचित्र 2.58 में बिन्दु आवेश q1 और q2 की वैद्युत क्षेत्र रेखाएँ दिखाई गई है। q1 और q2 के क्या-क्या चिह्न हैं? यदि रेखाएँ आवेश के अनुपात में खींची गईं हों, तो अनुपात q1/q2 क्या है?
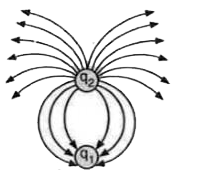 04:13View Solution
04:13View SolutionThree charges (-q1),(+q_(2)) And (-q_(3)) Are placed as shown in Figure I.1. Charge (-q_(1)) The x-component of the force is proportional to
03:22View Solutionचार आवेश q1=1μC,q2=2μC,q3=−3μC तथा q4=4μC,1 मी भुजा के वर्ग के शीर्षो पर रखे है। आवेशों के इस निकाय की वैद्युत स्थितिज ऊर्जा ज्ञात कीजिए।
07:49View Solution

