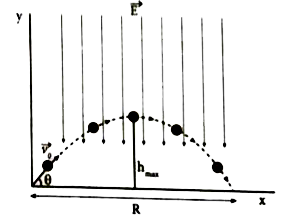
A small ball of conducting material having a charge +q and mass m is thrown upward at and angle θ to horizontal surface with an initial speed ν0 as shown in the figure. There exists an uniform electric field E downward along with the gravitational field g . Calculate the range maximum height and time of flight in the motion of this charged ball. Neglect the effect of air and treat the ball as a point mass .
 Solution in Tamil
Solution in Tamil
If the conductor has no net charge then its motion is the same as usual projectile motion of a mass m . Here in this problem in additionto downward gravitational force the charge also will experience a downward uniform electronstatic force.
The acceleration of the charged ball due to gravity =-g ˆj
The acceleration of the charged ball due to uniform electric field = −qEmˆj
The total acceleration of charged ball in downward direction →=−(g+qEm)ˆi
It is important here to note that the acceleration depends on the mass of the object . Galileo conclusion that all objects fall at the same rate towards the Earth is true only in a unifrorm gravitational field . When a uniform electric field is included the acceleration of a charged object depends on both mass and charge .
But still the acceleration a = (g+qEm) is constant through the motion. Hence we use kinematic equations to calculate the range maximum height and time of flight. In fact we can simply replace g by g+qEm in the usual expressions of range maximum height and time of flight of a projectile .

Note that the time of flight maximum height range are all inversely proprotional to the acceleration of object . Since (g+qEm)>g y for charge +q the quantities T, hmax and R will decrease when compared to the motion of an object of mass m and zero net charged. Suppose the charges is then (g−qEm)<g and the quantities T hmax and R will increase . Interestingly the trajectory is still parabolic as shown in the figure .

Topper's Solved these Questions
- ELECTROSTATICS BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - Textual Evaluation Solved (Multiple choice questions : )
15 Videos
- ELECTROSTATICS BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - Textual Evaluation Solved (II. Short Answer Questions : )
21 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - FULL MARKSCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ADDITIONAL QUESTIONS -( ADDITIONAL NUMERICAL PROBLEMS : )
10 Videos
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - ADDITIONAL QUESTIONS SOLVED - NUMERICAL PROBLEMS :
4 Videos
Similar Questions
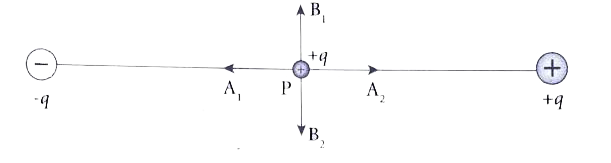
Two identical point charges'of magnitude -q are fixed as shown in the figure below. A third charge +q is placed midway between the two charges at the point P. Suppose this charge is displaced a small distance from the point P in the directions indicated by the arrows, in which direction(s) will +q be stable with respect to the displacement?
View SolutionWhat is meant by quantisation of charges ?
View SolutionIf a light of wavelength 4950 Å is viewed as a continuous flow of photons, what is the energy of each photon in eV ? (Given h=6.6×10−34Js, c =3×108ms−1)
View SolutionThe radius of the first orbit of hydrogen atom is 0.5 Å. The electron moves is an orbit with a uniform speed of 2.2×106ms−1. What is the magnetic field produced at the centre of the uncleus due to the mation of this electron ? Use μ0=4π×10−7Hm−1 and electric charge =1.6×10−19 C
View SolutionA charged particle of mass m=1 kg and charge q=2muC is thrown for a horizotal ground at an angle theta=45^@ with speed 20 m//s . In space a horizontal electric field E=2xx10^(7) V/m exist. Find the range on horizontal ground of the projectile thrown.
View SolutionA ball of mass m is thrown vertically upwards. Another ball of same mass is thrown at an angle theta to the horizontal. If the time if flights for both is same, the ratio of maximum height attained by them
View SolutionA ball of mass m having a charge q is released from rest in a region where a horizontal electric field E exists.
(a) Find the resultant force acting on the ball.
(b) Find the trajectory followed by the ball.
View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View SolutionA charged ball with mass m and charge q is dropped from a height h over a non-conducting smooth horizontal plane. There exists a uniform electric field E0 in vertically downward direction and the coefficient of restitution between the ball and the plane is e. Find the maximum height attained by the ball after nth collision.
View SolutionA particle of mass m and charge q is thrown with initial velocity v_(0) at an angle with the horizontal. In space there exist an electric field of strength E at angle beta with the downward vertical away from the point of projection. Find the time of flight and range of projectile on horizontal ground
View SolutionA charged ball of mass m and charge q is projected from the ground with an initail velocity u and angle of projection theta at the time of projection vertically upward electric field E is switched on. When it reaches the maximum height electric filed is switched off and a horizontal electric feild of same magnitude E is switched on. Then answer the following question (Assume mg> qE) Q If the time of flight to the maximum height is t_1 and the time of flight maximum height to the ground is t_2 then
View SolutionA block of mass m and positive charge q is placed on an insulated frictionless inclined plane as shown in the figure. A uniform electric field E is applied parallel to the inclined surface such that the block is at rest. Calculate the magnitude of the electric field E.
View SolutionA ball moving is thrown at an angle of 60^(@) with the horizontal , with initial speed of 30 m//s . Calculate (a) time of flight of the ball (b) hrizontal range . (c) maximum height attained .
View SolutionA ball is thrown in air at an angle 45^(@) and the other ball at an angle of 60^(@) . Calculate the ratio of maximum height and horizontal range of two balls .
View SolutionIn the figure shown a ball is suspended from the ceiling of a room in a uniform electric field of magnitude 2×104 V/m . If the mass of the ball is 25 g and the charge on the ball is 3μC . The angle θ is (g=9.8ms−2)

View Solution
