Two conducting spheres of radius r1 =8 cm and r2 =2 cm are separated by a distance much larger than 8 cm and are connected by a thin conducting wire as shown in the figure . A total charge of Q=+100 nC is placed on one of the spheres . After a fraction of a second the charge Q is redistributed and both the spheres attain electrostatic equilibrium .

(a) Calculate the charge and surface charge density on each sphere.
(b) Calculate the potential at the surface of each sphere . Solution in Tamil
( a) The electrostatic potential on the surface of the sphere A is VA=14πεllon0q1r1
The electrostatic potential on the surface of the sphere A is VB=14πε0q2r2
Since VA=VB. We have q1r1=q2r2⇒q1=(r1r2)q2
But from the conservation of total charge Q=q1+q2 we get q1=Q−q2. By substituting this in the above equation ,
Q−q2=(r1r2)q2 so that q2=Q(r2r1+r2)
Therefore q2=100×10−9×(210)=20nC and q1=Q−q2=80nC
The electric charge density for sphere A is σ1=q14πr21
The electric charge density for sphere B is σ2=q24πr22
Therefore σ1=80×10−94×64×10−4=0.99×10−6cm−2
and σ2=20×10−94π×4×10−4=3.9×10−6cm−2
Note that the surface charge density is greater on the smaller sphere compared to the larger sphere (σ2≈4σ1) which confirms the result σ1σ2=r2r1 .
The potential on both sphere is the same . So we can calculate the potential on any on of the spheres .
VA=14πε0q1r1=9×109×80×10−98×10−2=9kV
Topper's Solved these Questions
- ELECTROSTATICS BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - Textual Evaluation Solved (Multiple choice questions : )
15 Videos
- ELECTROSTATICS BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - Textual Evaluation Solved (II. Short Answer Questions : )
21 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - FULL MARKSCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ADDITIONAL QUESTIONS -( ADDITIONAL NUMERICAL PROBLEMS : )
10 Videos
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - ADDITIONAL QUESTIONS SOLVED - NUMERICAL PROBLEMS :
4 Videos
Similar Questions
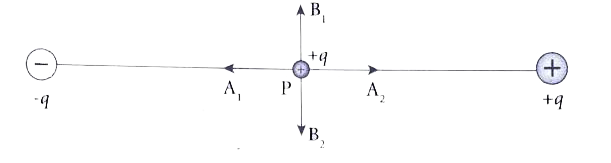
Two identical point charges'of magnitude -q are fixed as shown in the figure below. A third charge +q is placed midway between the two charges at the point P. Suppose this charge is displaced a small distance from the point P in the directions indicated by the arrows, in which direction(s) will +q be stable with respect to the displacement?
View SolutionWhat is meant by quantisation of charges ?
View SolutionIf a light of wavelength 4950 Å is viewed as a continuous flow of photons, what is the energy of each photon in eV ? (Given h=6.6×10−34Js, c =3×108ms−1)
View SolutionThe radius of the first orbit of hydrogen atom is 0.5 Å. The electron moves is an orbit with a uniform speed of 2.2×106ms−1. What is the magnetic field produced at the centre of the uncleus due to the mation of this electron ? Use μ0=4π×10−7Hm−1 and electric charge =1.6×10−19 C
View SolutionA solid conducting sphere of radius 10 cm is enclosed by a thin metallic shell of radius 20 cm . A charge q = 20 mu C is given to the inner sphere is connected to the shell by a conducting wire.
View SolutionConsider two conducting spheres of radill R_(1) and R_(2) with R_(1) gt R_(2) . If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whether the charge density of the smaller sphere is more or less than that of the larger one.
View SolutionCharge q on a small conducting sphere S_(1) is placed inside a large hollow metallic sphere S_(2) having a charge Q as shown in figure. The sphere is connected to shell by a conducting wire. The charge on S_(1) will then be
View SolutionTwo conducting spheres of radius R and 3R carry charges Q and −2Q. Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The final charge on initially neutral conducting sphere is :
View SolutionTwo solid conducting spheres of radii R_(1) and R_(2) are kept at a distance d (gt gt R_(1) and R_(2)) apart. The two spheres are connected by thin conducting wires to the positive and negative terminals of a battery of emf V. Find the electrostatic force between the two spheres
View SolutionConsider two conducting spheres of radii R_(1) and R_(2) with R_(1) gt R_(2) . If the two are at same potential, the larger sphere has more charge than the smaller sphere, then charge density of the smaller sphere is more than that of the larger one.
View SolutionConsider two conducting spheres of radii R1andR2 with R1>R2. If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whetehr the charge density of the smaller sphere is more or less than that of the larger oe.
View SolutionTwo metallic spheres of radii a and b are placed faraway from each other and are connected for a thin conducting wire. A charge Q is given to one of the spheres . Calculate the charge on each sphere at electrostatic equilibrium.
View SolutionA conducting sphere S1 of radius r1 is connected by a conducting wire to another conducting sphere S2 of radius r2, where r1=3cmandr2=2 cm. Before they are connected, S1 carries charge of 10 units. The electric potential at the point which is at a distance 4 cm from the centre of S1 and a distance 3 cm from the centre of S2 is
View SolutionTwo equally charged spheres A and B with radii rAandrB(rA>rB) are connected by a conducting wire. Will the charge density on both the spheres become equal after connection?
View SolutionConsider two conducting spheres of radii R_(1) and R_(2) with R_(1) gt R_(2) . If the two are at the same potential, the larger sphere bas more charge than the smaller sphere. State whether the charge density of the smaller sphere is more or less than that of the larger one.
View Solution
