A solid conducting sphere of radius 10cm is enclosed by a thin metallic shell of radius 20cm. A charge q=20μC is given to the inner sphere is connected to the shell by a conducting wire.
12 J
9 J
24 J
zero
The correct Answer is:B
To solve the problem step by step, we will analyze the situation involving the solid conducting sphere and the thin metallic shell.
Step 1: Understand the System
We have a solid conducting sphere of radius r1=10cm=0.1m with a charge q=20μC=20×10−6C. This sphere is enclosed by a thin metallic shell of radius r2=20cm=0.2m. The conducting wire connects the inner sphere to the shell.
Step 2: Determine the Charge Distribution
Since the inner sphere is connected to the shell by a conducting wire, the charge will redistribute itself. The total charge q will be shared between the inner sphere and the outer shell. However, since the outer shell is neutral initially, it will acquire a charge of −q to maintain overall neutrality.
Step 3: Calculate the Potential Energy Change
The potential energy U of a charge q at a distance r from the center of a sphere is given by:
U=12⋅q24πϵ0r
We will calculate the potential energy for both the inner sphere and the outer shell.
1. Potential Energy of the Inner Sphere:
U1=12⋅q24πϵ0r1
2. Potential Energy of the Outer Shell:
U2=12⋅q24πϵ0r2
Step 4: Substitute the Values
Substituting the values into the equations:
- For r1=0.1m:
U1=12⋅(20×10−6)24πϵ0(0.1)
- For r2=0.2m:
U2=12⋅(20×10−6)24πϵ0(0.2)
Step 5: Calculate the Change in Potential Energy
The change in potential energy ΔU is given by:
ΔU=U1−U2
Step 6: Final Calculation
Substituting the values into the equation:
ΔU=12⋅(20×10−6)24πϵ0(10.1−10.2)
Now, using ϵ0=8.85×10−12C2/N m2:
ΔU=12⋅(20×10−6)24π(8.85×10−12)(10−5)
ΔU=12⋅(400×10−12)4π(8.85×10−12)⋅5
Calculating this gives:
ΔU=9J
Conclusion
The final answer is 9J.
We have a solid conducting sphere of radius r1=10cm=0.1m with a charge q=20μC=20×10−6C. This sphere is enclosed by a thin metallic shell of radius r2=20cm=0.2m. The conducting wire connects the inner sphere to the shell.
Since the inner sphere is connected to the shell by a conducting wire, the charge will redistribute itself. The total charge q will be shared between the inner sphere and the outer shell. However, since the outer shell is neutral initially, it will acquire a charge of −q to maintain overall neutrality.
The potential energy U of a charge q at a distance r from the center of a sphere is given by:
U=12⋅q24πϵ0r
We will calculate the potential energy for both the inner sphere and the outer shell.
U1=12⋅q24πϵ0r1
U2=12⋅q24πϵ0r2
Substituting the values into the equations:
- For r1=0.1m:
U1=12⋅(20×10−6)24πϵ0(0.1)
- For r2=0.2m:
U2=12⋅(20×10−6)24πϵ0(0.2)
The change in potential energy ΔU is given by:
ΔU=U1−U2
Substituting the values into the equation:
ΔU=12⋅(20×10−6)24πϵ0(10.1−10.2)
Now, using ϵ0=8.85×10−12C2/N m2:
ΔU=12⋅(20×10−6)24π(8.85×10−12)(10−5)
ΔU=12⋅(400×10−12)4π(8.85×10−12)⋅5
Calculating this gives:
ΔU=9J
The final answer is 9J.
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Comprehension
Explore 36 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Matrix Matching
Explore 2 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Integer
Explore 17 Videos
- ELASTICITYBook:DC PANDEY ENGLISHChapter:ELASTICITYExercise:Medical entrances s gallery
Explore 21 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
Similar Questions
A solid conducting sphere of radius a is enclosed in a concentric shell of radius b>a. The charge on the inner sphere is 3μC and on the conducting shell is −10μC. The potential difference between the conductors is V. If +10μC additional charge is given to the outer shell, the new potential difference is
A. V
B. V/2
C. 2V
D. zero
View SolutionFigure shows a solid conducting sphere of radius 1 m. enclosed by a metallic shell of radius 3 m such that their centress coincide. If outer shell is given a charge of 6 μC and inner sphere is earthed, find megnitude charge on the surface of inner shell

View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
The charge on solid sphere is
View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
The potential of outer shell is
View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
Pick up the correct statement.
View SolutionFigure shows a solid metal sphere of radius a surrounded by a concentric thin metal shell of radius 2a. Initially both are having charges Q each, When the two are connected by a conducting wire as shown in the figure, then amount of heat produced in this process will be :
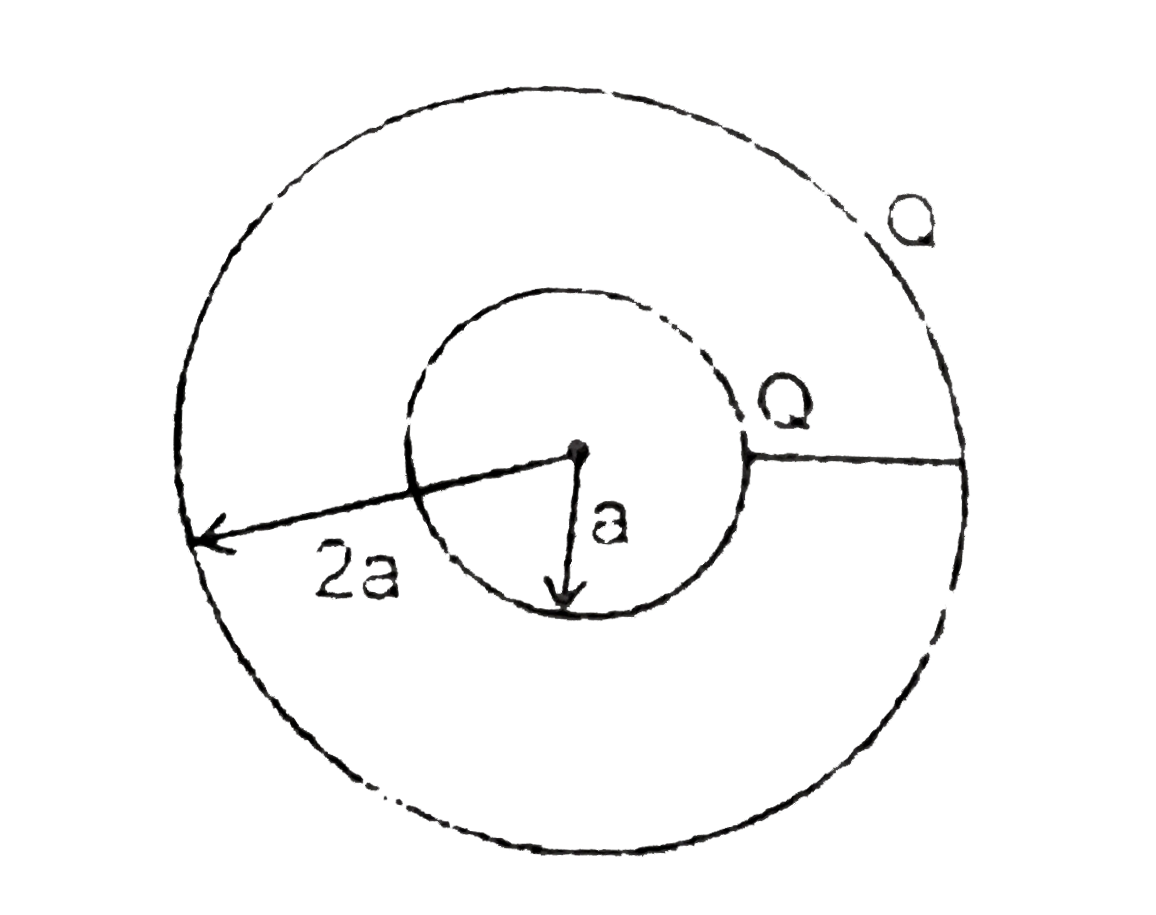
View SolutionA conducting sphere of radius R and a concentric thick spherical shell of inner radius 2R and outer radius 3R is shown in figure. A charge +10Q is given to the shell and inner sphere is earthed. Then charge on inner sphere is

View SolutionA conducting sphere of radius 10cm is charged 10μC. Another uncharged sphere of radius 20cm is allowed to touch it for some tome. After that if the sphere are separted, then surface density of chsrges, on the spheres will be in the ratio of
View SolutionTwo thin spherical shells made of metal are at a large distance apart. One of radius 10cm carries a charge of +0.5μC and the other of radius 20cm carries a charge of +0.7μC. The charge on each, when they are connected by a suitable conducting wire is respectively
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View Solution
