Derive an expression for potenstial energy of bar magnet in a uniform magnetic field.
 Solution in Tamil
Solution in Tamil
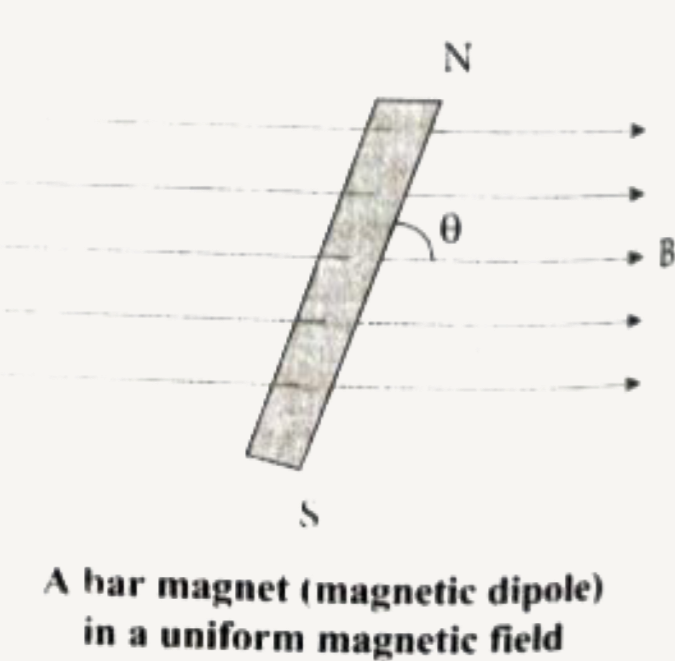
When a bar magnet (magnetic dipole ) of dipole moment −→Pm is held at an angle θ with the direction of a uniform magnetic field B , The magnetitude of the torque acting on the dipole is
∣∣→τB∣∣=∣∣∣−→Pm∣∣∣∣∣→B∣∣sinθ (1)
If the dipole is rotated through a very small angular displacement dθ against the torque τB at constant angular velocity , then the work done by external torque (−−→τext) for this small angular displacement is given by
dW = (−−→τext)dθ ....(2)
the bar magnet has to be moved at constant angular velocity, which implies that
∣∣→τB∣∣=∣∣−−→τexl∣∣
dW = PmBsinθdθ
Total work done in rotating the dipole from θ. to θ is
W=∫θθτdθ=∫θθ.PmBsinθdθ=pmB[−cosθdθ]θθ.
W = PmB(cosθ−cosθ.) .... (3) e
This work done is stored as potential energy in ber magnet at an angle θ when it is rotated from θ to θ and it can be written as ,
U=−PmB(cosθ−cosθ.) ... (4)
In fact, the equation (4) gives the difference in potential energy between the angular positions θ.andθ. we can choose the reference point θ.=90∘ , so that second term in the equation becomes zero and the equation 4 can be written as
U = −PmB(cosθ) ....(5)
U= -→pm∙→B
Case 1
(i) If θ=0∘,then
U = −pmB(cosθ∘)=−pmB
(ii) Ifθ=180∘, then
U = -pmB(cos180∘)=pmB
The potential energy stored in a bar magnet in a uniform magnetic field is given by
Topper's Solved these Questions
- BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - ADDITIONAL QUESTIONS SOLVED - NUMERICAL PROBLEMS :4videos
MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT
- BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - ADDITIONAL QUESTIONS SOLVED - 3-MARK QUESTIONS4videos
MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT
- BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - ADDITIONAL QUESTIONS SOLVED ( VII. NUMERICAL PROBLEMS )5videos
ELECTROSTATICS
- BOOK - FULL MARKSCHAPTER - OPTICSEXERCISE - ADDITIONAL QUESITON - II ADDITIONAL PROBLEMS:11videos
OPTICS
Similar Questions
The radius of the first orbit of hydrogen atom is 0.5 Å. The electron moves is an orbit with a uniform speed of 2.2×106ms−1. What is the magnetic field produced at the centre of the uncleus due to the mation of this electron ? Use μ0=4π×10−7Hm−1 and electric charge =1.6×10−19 C
02:01View SolutionExplain Curie's law of magnetism.
02:40View SolutionElectrons are caused to fall through a potential difference of 1500 volts. If they were initially at rest. Then calculate their final speed.
02:29View SolutionLight from a point source in air falls on a spherical glass surface (n = 1.5 and radius of curvature = 20 cm ). The distance of the light source from the glass surface is 100 cm. At what position the image is formed ?
03:31View SolutionA bar magnet is placed in a uniform magnetic field with its magnetic moment making an angle θ with the field. Write expressions for torque on the bar magnet and potential energy of magnet in this orientation. When it this energy minimum?
03:37View SolutionDerive an expression for torque acting on a bar magnet held at an angle with the direction of a uniform magnetic field.
05:30View SolutionFind expression for work done in rotating a bar magnet in a uniform magnetic field.
03:51View SolutionDerive an expression for potenstial energy of bar magnet in a uniform magnetic field.
 04:34View Solution
04:34View SolutionDerive an expression for potential energy of a bar magnet, when placed in uniform magnetic field.
05:38View SolutionDerive an expression for magnetic potential energy .for a magnetic dipole kept in a uniform magnetic field.
03:25View SolutionDerive an expression for torque acting on a bar magnet placed in a uniform magnetic field.
03:12View SolutionDerive an expression for Torque acting on a bar magnet placed in a uniform magnetic field.
06:48View SolutionDerive an expression for the time period of a magnet vibrating in a uniform magnetic field.
03:18View SolutionDerive an expression for magnetic potential energy for a magnetic dipole freely suspended in a uniform magnetic field B.
05:36View SolutionDerive an expression for a torque acting on a bar magnet placed in uniform magnetic field B.
View Solution

