Derive an expression for potential energy of a bar magnet when placed in an external magnetic field.
Video Solution
Text Solution
Potential of a bar magnet. The torque →τ acting on a magnetic dipole placed in a uniform magnetic field →B is given by :
→τ=→M×→B
or τ=MBsinθ ...(1)
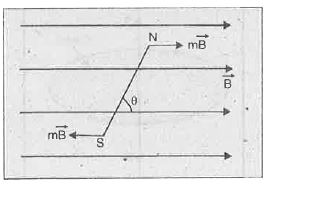
This torque tends to align the magnetic dipole in the direction of →B. If the dipole is rotated against the action of this torque, work has to be done, which is stored in the form of potential energy of the dipole.
Work done in rotating the dipole through an angle dθ against the torque is given by
dW=τdθ=MBsinθdθ
If the magnetic dipole is rotated from θ1andθ2, total work done will be
W=∫dW=MB∫θ2θ1sinθdθ
= −MB(cosθ2−cosθ1)
This work done is the energy stored U
∴ U=−MB(cosθ2−cosθ1)
If the dipole is rotated from
θ1=90∘ to θ2=θ then
U=−MB(cosθ−cos90∘)
U=−MBcosθ
or U=−→M⋅→B.
|
Topper's Solved these Questions
- MAGNETISMBOOK - MBD -HARYANA BOARDCHAPTER - MAGNETISMEXERCISE - LONG ANSWER TYPE QUESTIONS
7 Videos
- MAGNETISMBOOK - MBD -HARYANA BOARDCHAPTER - MAGNETISMEXERCISE - OBJECTIVE TYPE QUESTIONS
17 Videos
- MAGNETISMBOOK - MBD -HARYANA BOARDCHAPTER - MAGNETISMEXERCISE - OBJECTIVE TYPE QUESTIONS
17 Videos
- ELECTROSTATICSBOOK - MBD -HARYANA BOARDCHAPTER - ELECTROSTATICSEXERCISE - OBJECTIVE TYPE QUESTIONS
23 Videos
- MODEL TEST PAPER (SOLVED)BOOK - MBD -HARYANA BOARDCHAPTER - MODEL TEST PAPER (SOLVED)EXERCISE - LONG ANSWER TYPE QUESTIONS
6 Videos
Similar Questions
Knowledge Check
When a bar magnet is placed in a non-uniform magnetic field, it performs
Arotational motion.Btranslational motion.Crectilinear motion.Dboth (A) and (B).A paramagnetic sample shows a net magnetization of 8Am−1 when placed in an external magnetic field of 0.6 T at a temperature of 4 K When the same sample is placed in an external magnetic field of 0.2 T at a temperature of 16 K, the magnetization will be
A323Am−1B23Am−1C6Am−1D2.4Am−1
A ferromagnetic material is placed in an external magnetic field. The magnetic domains
View SolutionWhat is the potential energy of a magnetic dipole when it is placed perpendicular to the magnetic field?
View SolutionDerive an expression for torque acting on a bar magnet held at an angle with the direction of a uniform magnetic field.
View SolutionWhat happens in domain of ferromagnetic material is placed in external magnetic field
View SolutionA ferromagnetic material is placed in an external magnetic field. The magnetic domains
View SolutionWhat is the potential energy of a dipole when it is perpendicular to a magnetic field?
View Solution
