Discuss the diffraction at a grating and obtain the condition for the nth maximum.
A plane transmission grating is reperented by AB. Let a plane wavefront of monochromatic light with wavelenght λ be incident normally on the grating. As the slits size is comparable to that of wavelenght, the incident light diffracts at the grating.
A diffraction patteern is obtained on the screen when the diffracted waves are focused on a screen using a convex lens. Let us consider a point P at an angle θ with the normal drwan from the center of the gratng t the screen. The path difference δ between the diffracted waves from one pair of corresponding points is, δ=(a+b)sinθ
This path difference is the same for any pair of corresponding points. The points P will be bright, when
δ=mλ where m = 0,1,2,3
Combining the above two equaitons, we get,
(a+b)sinθ=mλ
Here, m is called order of diffraction.
Condition for zero maximum, m = 0
For (a+b)sinθ=0. the position, θ=0,sin0=0andm=0. This is called zero order diffraction or central maximum.
Condition for second order maximum, m = 1,
If (a+b)sintˆa1=λ, the diffracted light meet at an angle θ1 to the incidet direction and the first order maximum is obtained.
Condition for second order maximum, m = 2
Similarly, (a+b)sinθ2=2λ forms the second order maximum at the angula positio θ2.
Condition for higher order maximum
On either side of central maxima different higher orders of diffraction maxima are formed at different angular position.
It we take, N=1a+b
Then, N gives the number of grating elements or rulings drawn per unit width of the grating. Normally, this number N is specified on the grating itselt. Now, the equation becomes,
1Nsinθ=mλ(or)sinθ=Nmλ

Topper's Solved these Questions
- OPTICSBOOK - FULL MARKSCHAPTER - OPTICSEXERCISE - TEXTUAL EVALUATION SOLVED IV.CONCEPTUAL QUESTION:
10 Videos
- OPTICSBOOK - FULL MARKSCHAPTER - OPTICSEXERCISE - TEXTUAL EVALUATION SOLVED V.NUMERICAL PROBLEMS
10 Videos
- OPTICSBOOK - FULL MARKSCHAPTER - OPTICSEXERCISE - TEXTUAL EVALUATION SOLVED SHORT ANSWER QUESTION
80 Videos
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - ADDITIONAL QUESTIONS SOLVED - NUMERICAL PROBLEMS :
4 Videos
- RECENT DEVELOPMENTS IN PHYSICSBOOK - FULL MARKSCHAPTER - RECENT DEVELOPMENTS IN PHYSICSEXERCISE - ADDITIONAL QUESTIONS (Short Answer Question)
6 Videos
Similar Questions
For diffraction to be observed, the main condition is
View SolutionA narrow beam of X-rays falls at a glancing angle of 20∘ on a diffraction grating with a constant of 2.0 μ m. The first diffraction maximum is observed at an angle of 12' to the direction of the beam. Find the wavelenght of the X-rays
View Solution
Knowledge Check
For diffraction to be observed, the main condition is
Athe size of an obstacle should be of the same order as the wavelengthBthe size of an obstacle should be very large as compared to the wavelength of light usedCthe size of an obstacle should be exactly λ/2Dthere should be no relation between the wavelength and the size of the obstacleFirst secondary minima in case of diffraction due to single slit is obtained at a distance x from central maximum position, then
Ax=λaDBxa=DλCx=λDaDx=λDaLight from a laser (λ=640nm) passes through a diffraction grating and spreads out into three beams as shown in the figure. Determine the spacing between the slits of the grating
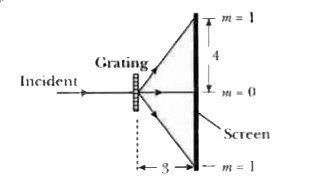 A240 nmB680 nmC410 nmD800 nm
A240 nmB680 nmC410 nmD800 nm
Light with wavelength λ falls on a diffracting grating at right angles. Find the angular dispersion of the grating as a function of diffraction angle θ.
View SolutionA plane light wave with wavelength λ falls normally on a phase diffraction grating whose side view is shown in Fig. The grating is cut on a glass plate with refractive index n. Find the depth h of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. what is in this case the diffraction angle corresponding to the first maximum?
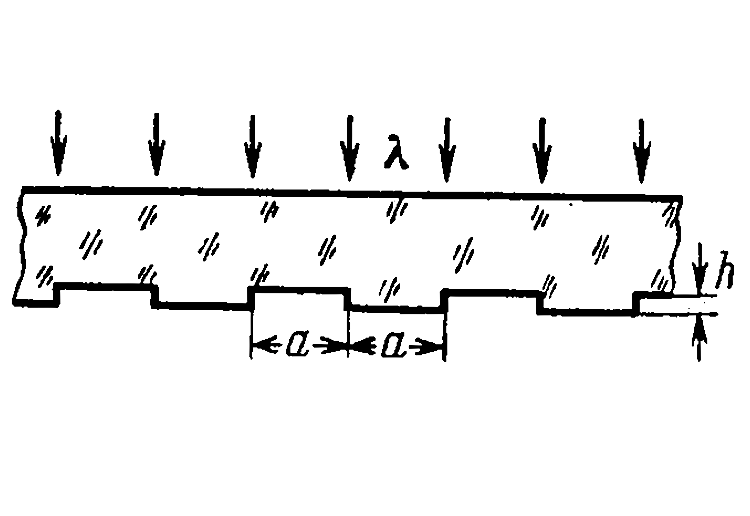
View SolutionA grating has 5.7×103 lines per cm. If X-rays of wavelength 546 nm are incident on the grating, find the angle of reflection for the first order diffraction maximum.
View SolutionSodium light of wavelength 5890 Å is incident normally on a diffraction grating of 5000 rulings per cm. Find the angle of diffraction for the second order.
View SolutionWhat is the condition for diffraction to take place ?
View Solution
