Explain the J.J. Thomson experiment to determine the specific charge of electron.Solution in Tamil
In 1887, J. J. Thomson made remarkable improvement in the scope of study of gases in discharge tubes. In the presence of electric and magnetic fields, the cathode rays are deflected. By the variation of electric and magnetic fields, mass normalized charge or the specific charge (charge per unit mass) of the cathode rays is measured.

A highly evacuated discharge tube is used and cathode rays (electron beam) produced at cathode are attracted towards anode disc A. Anode disc is made with pin hole in order to allow only a narrow beam of cathode rays. These cathode rays are now allowed to pass through the parallel metal plates, maintained at high voltage. Further, this gas discharge tube is kept in between pole pieces of magnet such that both electric and magnetic fields are perpendicular to each other. When the cathode rays strike the screen, they produce scintillation and hence bright spot is observed. This is achieved by coating the screen with zinc sulphide.
(1) Determination of velocity of cathode rays For a fixed electric field between the plates, the magnetic field is adjusted such that the cathode rays (electron beam) strike at the original position O. This means that the magnitude of electric force is balanced by the magnitude of force due to magnetic field. Let e be the charge of the cathode rays, then
eB=eBv

(ii) Determination of speelfie charge
Since the cathode rays (electron beam) are accelerated from cathode to anode, the potential energy of the electron beam at the cathode is converted into kinetic energy of the electron beam at the anode. Let V be the potential difference between anode and cathode, then the potential energy is eV. Then from law of conservation of energy,
Substituting the value of velocity from equation (1), we get
Substituting the values of E, B and V, the specific charge can be determined as
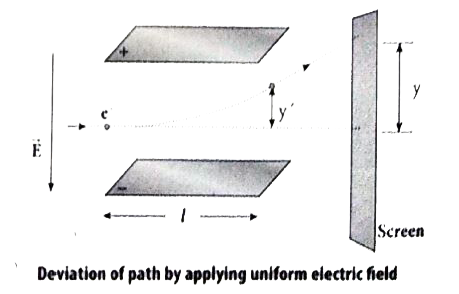
(iii) Deflection of charge only due to uniform electric field When the magnetic field is turned off, the deflection is only due to clectric field. The deflection in vertical direction is due to the electric force.
Let m be the mass of the electron and by applying Newton.s second law of motion, acceleration of the clectron is
Substituting equation (4) in equation (3).
Let y be the deviation produced from origianal position on the screen. Let the initial upward velocity of cathode ray be u=0 before entering the parallel electric plates. L t be the time taken by the cathode rays to travel in electric field. Let l be the length of one of the plates, then the time taken is
Hence the deflection y. of the cathode rays is (note: u=0 and
Therefore, the deflection y on the screen is
where C is proportionality constant which depends on the geometry of the discharge tube and substituting y. value in equation (6), we get
Rearranging equation (7) as
Substituting the values on RHS, the value of specific charge is calculated as
(iv) Deflection of charge only due to uniform magnetic field Suppose that the electric field is switched off and only the magnetic field is switched on. Now the deflection occurs only due to magnetic field. The force experienced by the electron in uniform magnetic field applied perpendicular to its path is
Since this force provides the centripetal force, the electron beam undergoes a semicircular path. Therefore, we can equate to centripetal force
where v is the velocity of electron beam at the point where it enters the magnetic field and Ris the radius of the circular path traversed by the electron beam.
Further, substituting equation (1) in equation (9), we get
By knowing the values of electric field, magnetic field and the radius of circular path, the value of specific charge can be calculated.
Topper's Solved these Questions
Similar Questions
Write down Coulomb 's law in vector form and mention what each term represents .
View SolutionDerive an expression for electrostatic potential energy of the dipole in a uniform electric field .
05:11View SolutionDefine capacitance . Give its unit.
05:36View SolutionJ.J Thomson discovered nucleus.
01:08View SolutionIn J.J. Thomson e/m experiment, a beam of electron is replaced by that of muons (particle with same charge as that of electrons but mass 208 times that of electrons). No deflection condition is achieved only if
05:11View SolutionExplain the J.J. Thomson experiment to determine the specific charge of electron.
05:36View SolutionJ.J Thomson discovered ___________ .
05:11View SolutionIn J.J. Thomson e/m experiment, a beam of electron is replaced by that of muons (particle with same charge as that of electrons but mass 208 times that of electrons). No deflection condition is achieved only if
05:36View SolutionExplain the J.J. Thomson experiment to determine the specific charge of electron.
05:11View SolutionIn J.J. Thomson e/m experiment, a beam of electron is replaced by that of muons (particle with same charge as that of electrons but mass 208 times that of electrons). No deflection condition is achieved only if
04:32View SolutionExplain the J.J. Thomson experiment to determine the specific charge of electron.
03:25View SolutionIn J.J. Thomson e/m experiment, a beam of electron is replaced by that of muons (particle with same charge as that of electrons but mass 208 times that of electrons). No deflection condition is achieved only if
02:22View SolutionThe ratio of charge to mass of an electron in coulombs per gram was determined by J.J. Thomson. He determined this ratio by measuring the deflection of cathode rays in electric and magnetic fields. What value did he find for this ratio?
02:38View SolutionIn the J.J. Thomson method for the determination of e/m, what is the angle between the magnetic and electric fields to which the electrons are subjected ?
02:23View SolutionNature of the parabolic trajectory of the +VE ions in the J.J. Thomson experiment
53:14View Solution

