Calculate the magnetic induction at a point on the axial line of a bar magnet.Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Magnetic field at a point along the axial line of the magnetic dipole (bar magnet):
Consider a bar magnet NS. Let N be the North Pole and S be the south pole of the bar magnet, each of pole strength $q_{m}$ and separated by a distance of 2l. The magnetic field at a point C (lies along the axis of the magnet) at a distance from the geometrical center O of the bar magnet can be computed by keeping unit north pole $(q_{M C} = 1 Am)$ at C. The force experienced by the unit north pole at C due to pole strength can be computed using Coulomb.s law of magnetism as follows:
The force of repulsion between north of the bar magnet and unit north pole at point C (in free space) is ${\to F}_{N} = \frac{μ_{0}}{4 π} \frac{q_{m}}{(r - 1)} ˆ i ... ... ... ... (1)$
where r-l is the distance between north pole of the bar magnet and unit north pole at C.
The force of altration between South Pole of the bar magnet and unit North Pole at point C (in free space) is $v e F_{S} \frac{q_{m}}{{(r + l)}^{2}} ˆ l ... ... ... . . (2)$
where r+1 is the distance between south pole of the bar magnet and unit north pole at C.

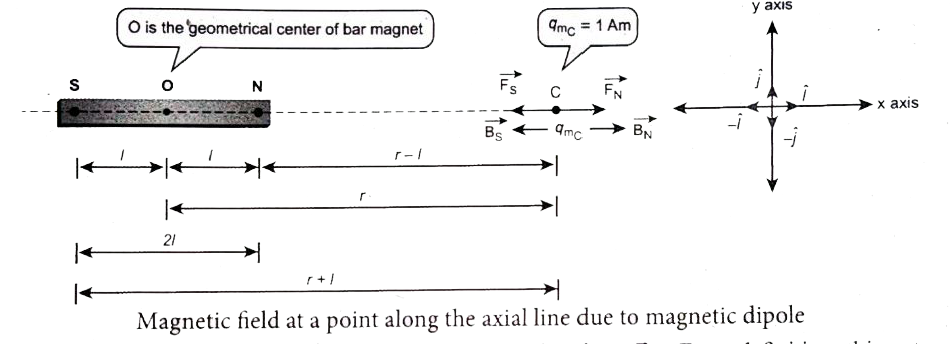
From equation (1) and (2), the net force at point C is $\to F = {\to F}_{N} + {\to F}_{S}$ . From definition, this net force is the magnetic field due ot magnetic dipole at a point $C (\to F = \to B)$
$\to B = \frac{μ_{0}}{4 π {(r - l)}^{2}} ˆ i + (\frac{μ_{0}}{4 π} \frac{q_{m}}{{(4 + l)}^{2}} ˆ i) = \frac{μ_{0} q_{m}}{4 π} (\frac{1}{{(r - l)}^{2}} - \frac{1}{{(r + l)}^{2}}) ˆ i \Rightarrow \to B = \frac{μ_{0} 2 r}{4 π} (\frac{q_{m} . (2 l)}{{(r^{2} - l^{2})}^{2}}) ˆ i ... ... ... . (3)$
Since, magnitude of magnetic dipole moment is $| {\to p}_{m} | = p_{m} = q_{m} .2 l$ the magnetic field point C equation (3) can be written as
${\to B}_{axial} = \frac{μ_{0}}{4 π} (\frac{2 r p_{m}}{{(r^{2} - l^{2})}^{2}}) ˆ i ... ... ... . . (4)$
If the distace between two poles in a bar magnetic are small (looks like short magnet) compared to the distance geometrical centre O of hte bar magnet and the location of point C i.e,
$r > > 1 then {(r^{2} - l^{2})}^{2} \approx r^{4} ... ... ... ... . (5)$
Therefore, using equation (5) in equation (4), we get
${\to B}_{axial} = \frac{μ_{0}}{4 π} (\frac{2 r p_{m}}{r^{3}}) ˆ i = \frac{μ_{0}}{4 π} \frac{2}{r^{3}} {\to p}_{m}$
Where ${\to p}_{m} = p_{m} ˆ i . ... ... ... ... (6)$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

FULL MARKS-SAMPLE PAPER-2 (SOLVED)-Part -IV

Home
Ask Doubt
Profile